[XCS224N] Lecture 4 – Backpropagation

More Matrix Gradients

⇒

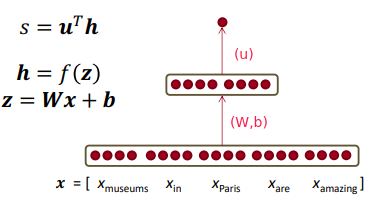
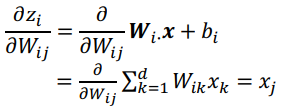
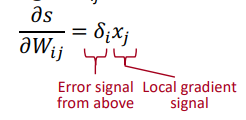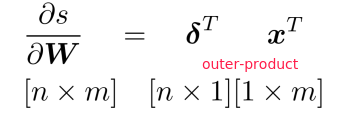
Deriving Gradients wrt Words

pitfall in tetraining word vectors: if some word is not in training data, but other synonyms are present ⇒ only the synonyms word vectors are moved

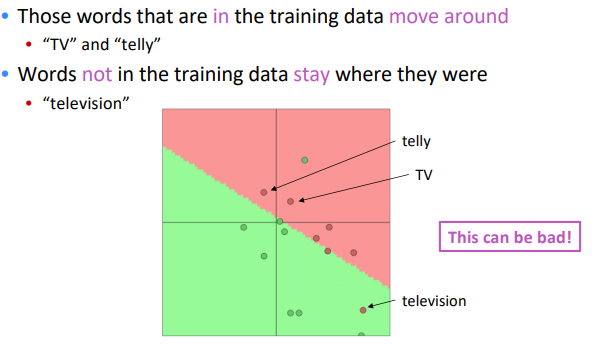
takeaway:

Backpropagation

backprop:

• apply (generalized) chain rule
• re-use shared stuff

computation graph

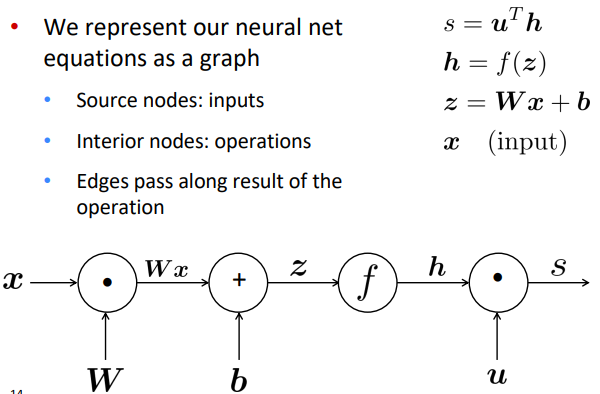
⇒ Go backwards along edges, pass along gradients

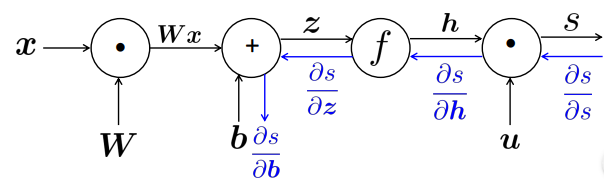
receive upstream grad => compute downstream grad

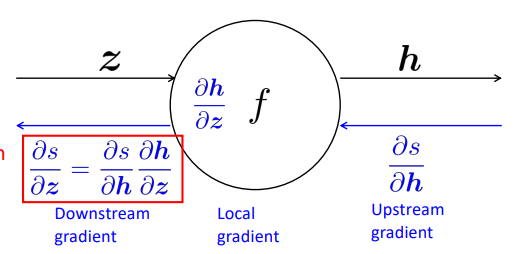
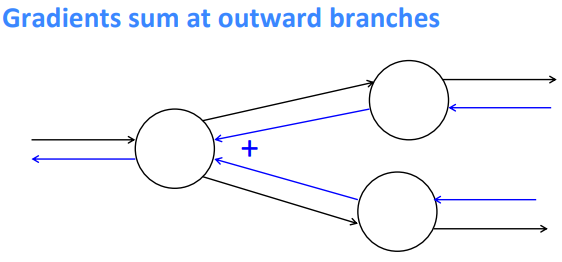
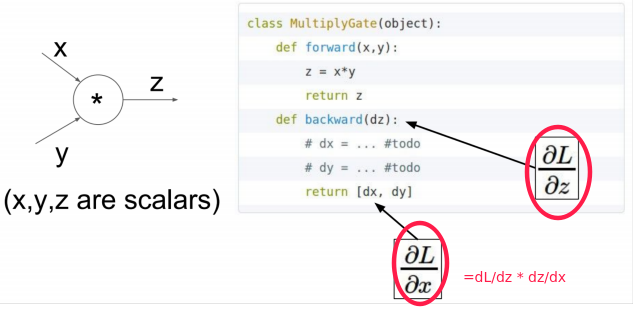
for node with multiple inputs:

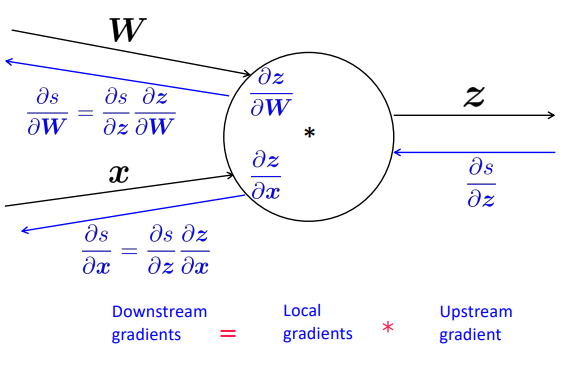
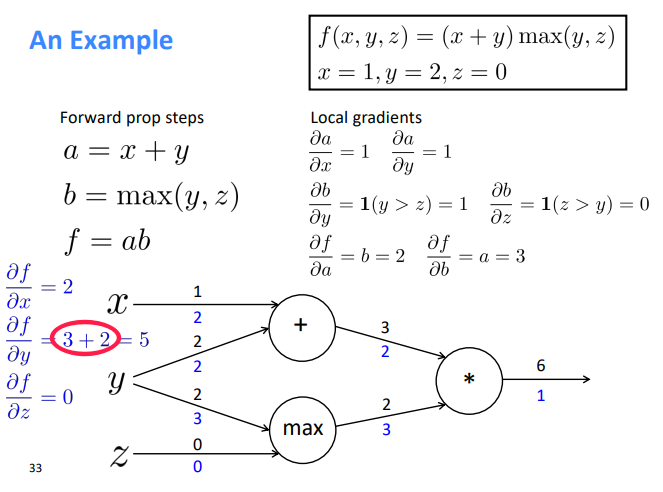
More on Backpropagation

intuition:

• plus( + ) distributes upstream grad

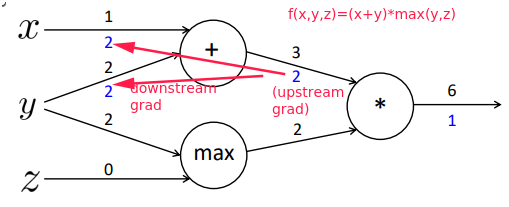
• maxroutes upstream grad

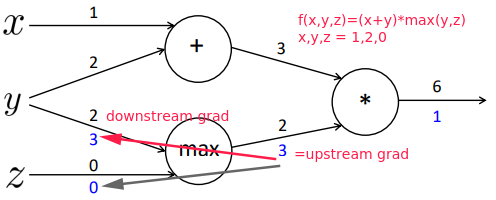
• multiply( * ) switches the upstream grad

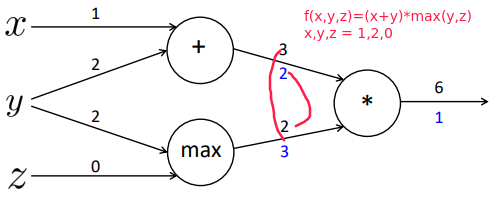
efficency: compute shared part once

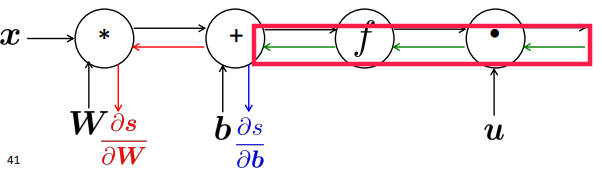
Backprop in general computation graph

comput-graph is a DAG ⇒ topological sort

• Fprop: visit nodes in topological
• Bprop: in reverse topological order

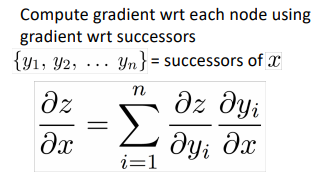
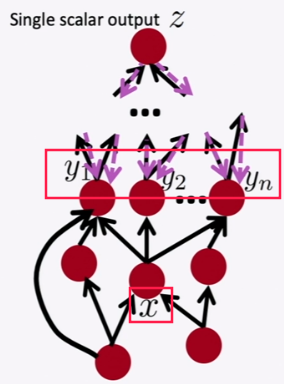
Complexity = O(n) Automatic Differentiation: symbolic computation on the symbolic expression of Fprop. Moden DL framework: must provide the Fprop/Bprop formular for each node.

Backprop Implementations

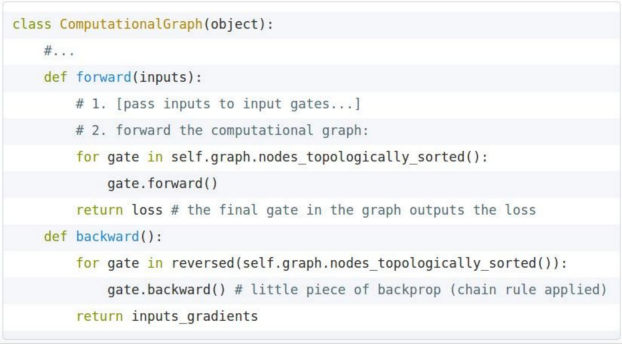
for each gate, impl the forward/backward API:

Numeric Gradient For checking if the forward/backward impl is correct e.g.check

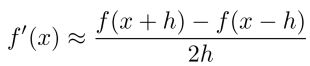
(note: use two-sided gradient checks)

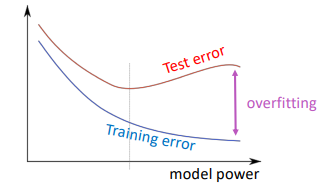
Regularization

Regularization term added to loss func to prevent overfitting:

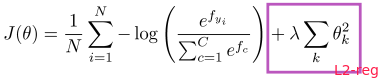
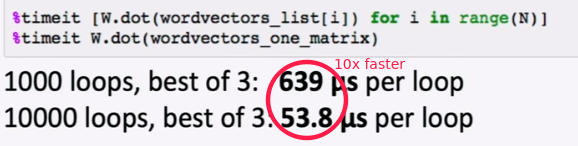
Vectorization/tensorization

avoid forloops, use matrix multiplication instead.

Nonlinearities

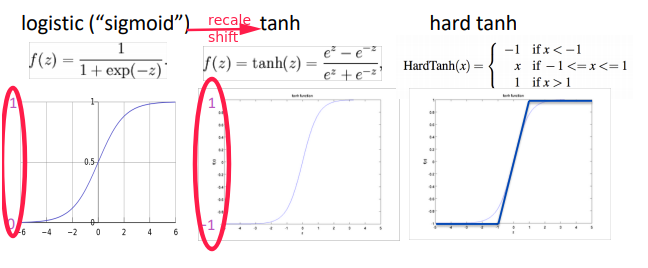
tanh is recaled and shifted of sigmoid: tanh(x) = 2 * sigmoid(2x) - 1

new world activation func:

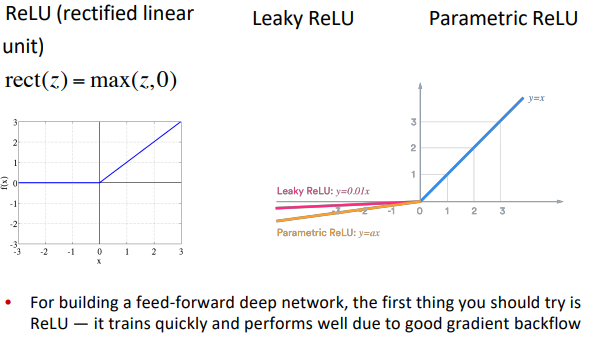
Parameter Initialization

Initialize the weights to small, random values ⇒ break the symmetry.

• Init bias to 0
• Init all other weights to Uniform(-r, r).
• Xavier initialization: variance inverse-proportional to sum of prev&next layer size

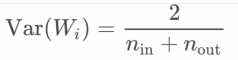
Optimizers and Learning Rates

Usually simple SGD works fine, but needs to tune the learningrate (lr). adaptive optimizers: per-parameter learning rate.

learning rate:

• try with powers of 10
• learningrate-decay:

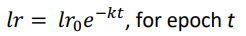
(epoch = full pass over the training data)