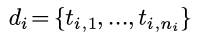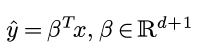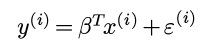之前一直用weka的GUI界面做机器学习的任务, 感觉这个软件虽然界面丑, 不过确实是快速开展机器学期的利器. 关于GUI的weka使用以后有时间再写. 今天这篇记录一下最近使用的java版本的weka.

1. Include jars into project

weka官网的下载链接里选择linux版本的weka压缩包即可, 下载以后找到weka.jar文件, 在工程里将其include一下就可以使用了(btw, 现在开始放弃eclipse, 进入IDEA的怀抱了...).

weka的文档在解压缩的文件里有, 另外在线文档在: http://weka.sourceforge.net/doc.stable-3-8/

about libsvm...

关于libsvm需要有一点特别指出. weka自带的算法里是不包含libsvm的 (有个类似的SMO, 不过还是libsvm久经考验啊...), 需要使用weka的package manager安装. 打开package manager是在weka主界面的菜单里:

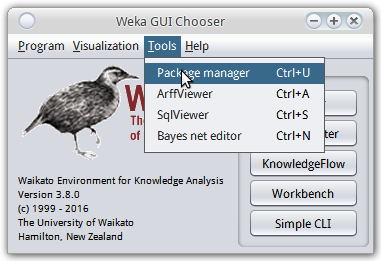
在package manager里搜索到libsvm安装即可. 然后(linux下)在主目录可以看到有个wekafiles文件夹, wekafiles/packages/LibSVM/目录下就是libsvm的内容.

需要指出的一点是, 要使用libsvm的话, 需要同时引用两个jar文件, 而且都叫libsvm.jar!!

这两个jar ...

除了上次介绍的minhash方法以外, 还有一种常见的hash方法, 叫做simHash. 这里做简要介绍.
这个hash函数的背景和上次一样, 还是考虑把文本抽象为ngram的集合:

然后相似度依旧是Jaccard similarity:

simHash

simHash的方法听上去比minHash还要简单:

1. 对一个文档d中的每一个term(ngram, shingle) t, 计算其hashcode(比如用java内建的Object.hashCode()函数) hash(t).
2. 把d中所有term的hash(t)合成为一个hashcode作为d的hashcode simHash(d): simHash(d)的长度与hash(t)相同, simHash(d)的第k个bit的取值为所有hash(t)第k个bit的众数.

写成数学表达式很吓人, 其实只不过不断在{0,1}和{-1 ...

approximate retrieval(相似搜索)这个问题之前实习的时候就经常遇到: 如何快速在大量数据中如何找出相近的数据.

问题描述: 假设有N个数据, 并且对于他们有一个相似度(或距离)的度量函数sim(i,j), 我们的问题就是如何快速找出所有N个点中相似度较大的i和j组合.

乍一看这个问题必须要对所有的(i,j)计算相似度, 但是N^2的复杂度在N太大的情况下是不能够忍受的.

kdtree

之前在algo-note里面遇到过kdtree, 用它可以使得寻找nearest neighbor的复杂度减少到logN. 但是这种情况对于维度低一点(比如二三维)的情况合适, 维度到了成千上万的时候并不是很好的选择, 所以这里不多讨论.

simhash

另一个思路是, 使用某个hash函数, 对于每一个数据计算一个哈希值. 这个hash函数要满足: 当i和j的相似度很高的时候, hash(i)和hash(j)的值(很可能)相同. 这次介绍的minHash就是这样的一种方法.

Jaccard similarity

明确问题含义, 首先需要定义相似度. 这里主要考虑文本相似度的问题, 假设字典D有M个term ...

几乎所有的ml课都是从线性回归讲起, ETH的课也不例外. 不过这次老师用了贝叶斯的视角讲这个问题, 自从高中接触丁老师讲的线性回归以来 第一次听到一个不同于最小二乘的解读, 感觉很有意思. 又想起来刘未鹏那篇非常棒的博客, 于是想记录一下.

notation

首先有n个数据点:

其中y是实数, 每个x有d个维度, 为了方便表示截距, 再给x加入一个始终等于1的维度:

例子: y代表房价, x代表了房子的面积, 使用时间, 距离市中心的距离等因素.

least square viewpoint

在最小二乘的视角里, 线性回归是用一个x的线性函数拟合y:

使得拟合结果和观测结果的误差尽量小.
不过这次不说最小二乘, 所以接下来不讨论这个思路...

assumptions in Bayes viewpoint

在贝叶斯视角里, 我们假设:
假设1. y = 某个x的线性函数 + 观测噪音
即:

其中εi是一个随机变量, 所以y也是一个随机变量.
另外再有一个比较强的假设:
假设2. ε服从centered高斯分布, iid.

(btw, 对一个随机变量建模, 一般来说, 连续随机变量就用高斯 ...