More on Word2Vec
parameters θ : matrix U and V (each word vec is a row):
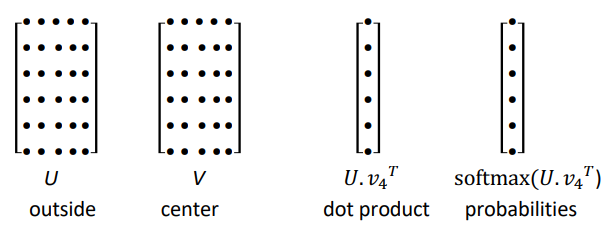
and the predictions don't take into account the distance between center word c and outside word o. ⇒ all word vecs predict high for the stopwords.
Optimization Basics
min loss function: J(θ)
gradient descent
direction of the gradient = direction where J(θ) increases the most.
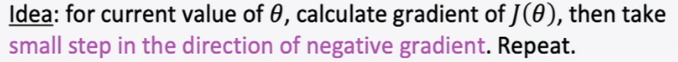

SGD
pb: J(θ) is for all words/positions in the corpus, grad J(θ) is very expensive to compute.
⇒ use random samples each time
⇒ each time we only sample one window of 2m+1 words


I.e.each time we compute the grad only on a minibatch. ⇒ each time we only update the wordvecs that appear in the minibatch.
Word2Vec: Model Variants
final embedding of a word = average of u and v
⇒ we can also do only one vec per word, not much difference
2 main varaints of w2v family:
- skip-grams(SG): predict outside word o with center word c:
P(o|c).← presented in the class. - continuous bag-of-words (CBOW): predict center word c using outside words o.
negative sampling
So far: naive sotfmax, i.e.sum over all words in vocab — expensive.
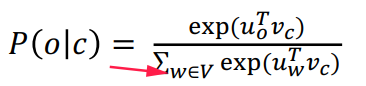
⇒ negative sampling. Use several binary logistic regressions on:
- the true pair (center word and a true context word )
- several nois pairs (center word and a random word) ← random negative pair
logistic regression = softmax with vocab size=2 sigmoid function: from inner-product value to probability score
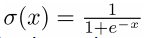
⇒ objective funcion (to maximize):
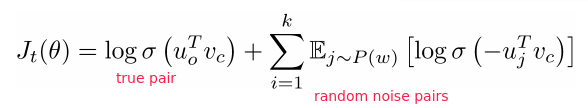
where P(w) is the distribution of negative sampling.
in practice: P(w)=U(w)^(3/4) i.e.3/4 power of the uniform distribution → makes rare words appear more often.
⇒ loss function (to minimize):
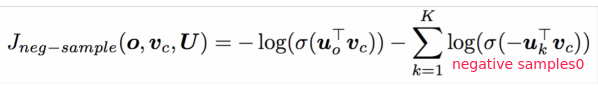
QUESTION: why put the minus inside the logit?
Alternative Methods: cooccurrence counts
Why not using co-occurrence counts matrix?
- co-occurrence in windows
- co-occurrence in document
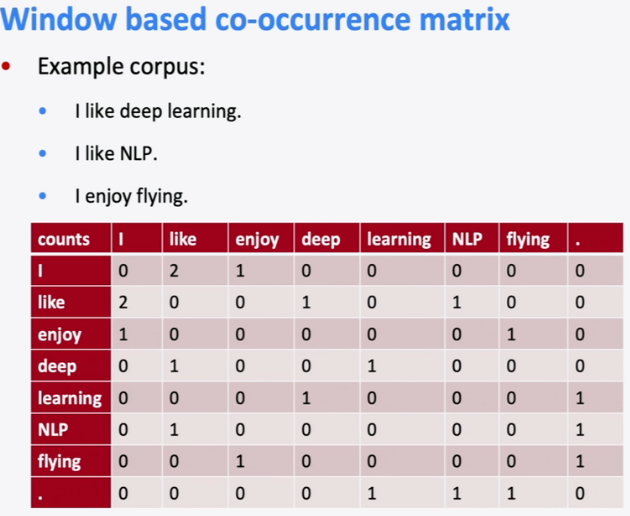
problems with co-occurrence matrix:
- matrix size increase with vocab size
- high dimensional, expensive storage
- Subsequent classification models have sparsity issues
⇒ model less robust
solution1: low-dimensional vectors
(signular value decomposition for k-largest eigen values)
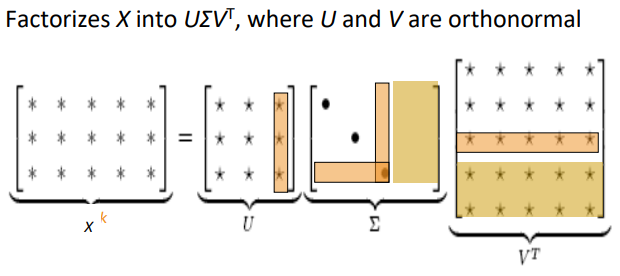
⇒ popular in the year 2000.
solution2: hacks to co-occurrence matrix
- trim stopwords
- counter more on closer words
- Pearson correlations to replace counts
comparison
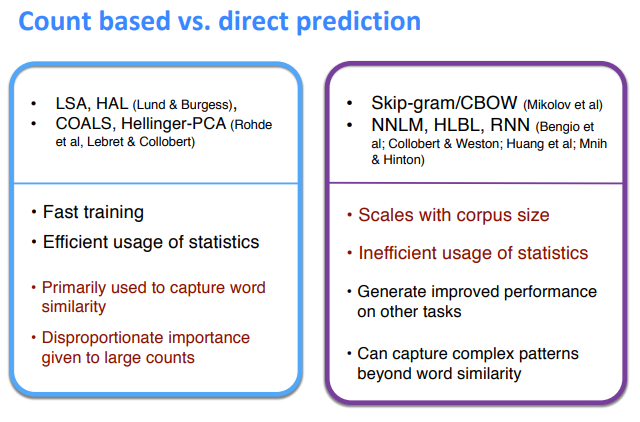
encode meanings
insight: ratios of co-occurrence probabilities can encode meaning.
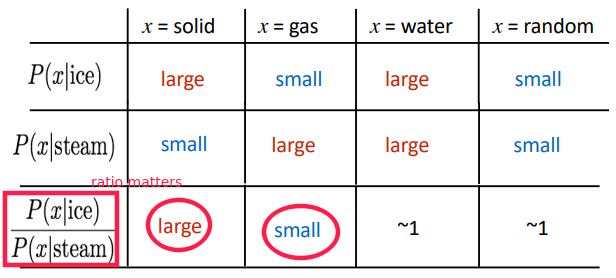
⇒ make dot-products equal to the log of co-occurence prabability ⇒ vector diff gives the ratio of co-occur proba

GloVe
Combine the best of both worlds: count method and prediction method.
log-bilinear: 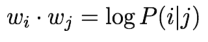
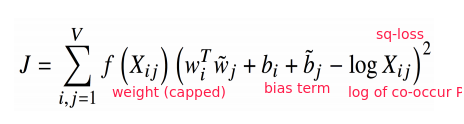
Where the weight ter f(Xij) is capped:
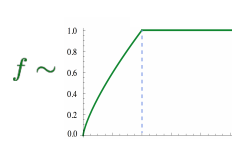
- Fast training
- Scalable to huge corpora
- Good performance even with small corpus and small vectors
Evaluating Word Vectors
Intrinsic vs extrinsic in NLP-eval: Intrinsic:
- Eval on a specific/intermediate subtask: e.g.word similarity, POS tag, etc.
- Fast to compute
- Not clear if really helpful unless correlation to real task is established
Extrinsic:
- Eval on real task: e.g.web search / question-answering / phone dialog
- Hard to run
- Hard to diagnois
⇒ today: focus on intrinsic word vector evaluation
Eval on word Analogies

- Semantic eval: city-in-state (e.g."Chicago Illinois Houston Texas")
- Syntactic eval: gram4-superlative (e.g."bad worst big biggest")
Hyperparameters:
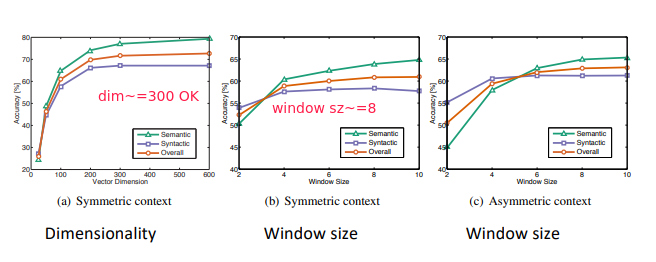
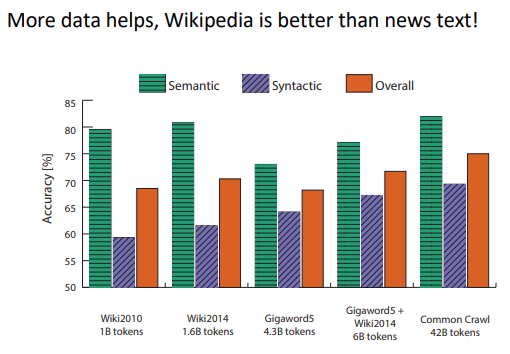
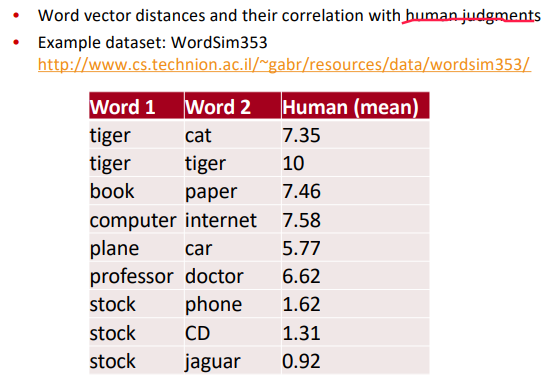
Eval on word Similarities
Word Senses
sense ambiguity: words have lots of meanings
- crude solution(2012): for each common word, find clusters of context that it occurs, split the word into pesudowords.
- Linear Algebraic Structure solution (2018):
word sense is a linear superposition:

⇒ result: Because of ideas from sparse coding you can actually separate out the senses (providing they are relatively common) actual word/sense are very sparse
Extrinsic word vector evaluation: e.g. NER (finding person/organization/location)
Part 2 of series «XCS224N: NLP with deep learning»:
- [XCS224N] Lecture 1 – Introduction and Word Vectors
- [XCS224N] Lecture 2 – Word Vectors and Word Senses
- [XCS224N] Lecture 3 – Neural Networks
- [XCS224N] Lecture 4 – Backpropagation
- [XCS224N] Lecture 5 – Dependency Parsing
- [XCS224N] Lecture 6 – Language Models and RNNs
- [XCS224N] Lecture 7 – Vanishing Gradients and Fancy RNNs
- [XCS224N] Lecture 8 – Translation, Seq2Seq, Attention
Disqus 留言