[XCS224N] Lecture 1 – Introduction and Word Vectors

Course intro

Word Meaning and Representation

denotational semantics

wordnet (nltk): word meanings, synonym, relationships, hierarchical

pb: missing nuance, missing new meanings, required human labor, can't compute word similarity

Traditional NLP (untill 2012):

• each words are discrete symbols — "localist representation"
• use one-hot vectors for encoding

• pbs with one-hot vecotrs:
• large dimension size
• each two words are orthogonal, no relationships between them

distributional semantics: A word’s meaning is given by the words that frequently appear close-by. ⇒ Use the many contexts of w to build up a representation of w.

"distributed representation": use dense vectors for each word, so that it is similar to vectors of words that appear in similar contexts.

Word2Vec Introduction

word2vec algo: for learning word embeddings.

idea

• start with large text corpus
• each word from the (fixed) vocab has a vector v — start with rand vectors
• for each center word c and context(outside) word o :
• use sim(c,o) to compute P(o|c) or P(c|o) .
• update the vecs to maximize the probability

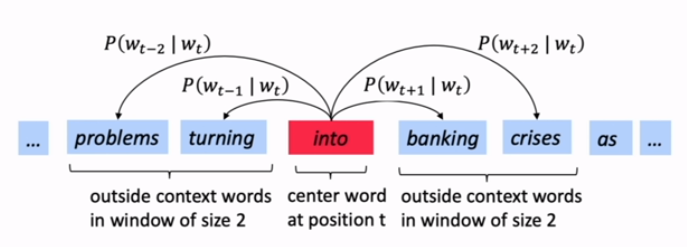
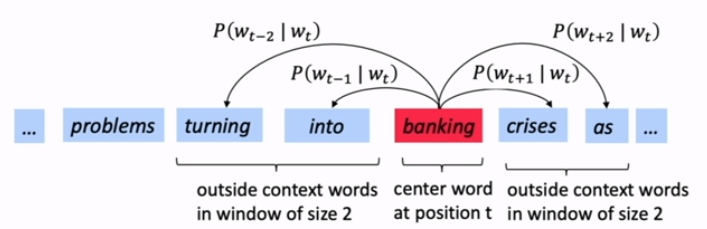
likelihood

Likelihood := product of all predicted probabilities for all window words (fixed window sz= m ), for all positions t .

Loss function

⇒ take negative log likelihood as loss function:

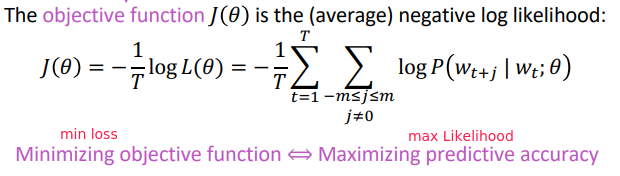
Prediction function

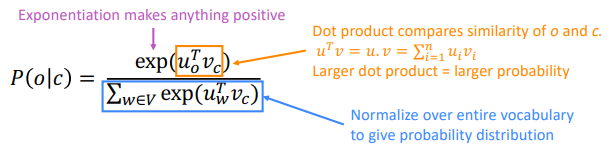
⇒ probability prediction P(o|c) is a function of the word vectors:

• we use two vectors per word:
• use v_w when word w is the center word
• use u_w when w is context word.
• proba = softmax of the dot products dot(v,u) for all context word u in Vocab.

optimization

θ :=all parameters in the model, i.e. 2*V vectors (u/v), each of dimension d .

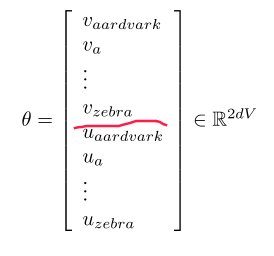
gradient descent: compute all gradients of θ w.r.t.loss function J(θ) . I.e.compute dJ(θ)/dθ, which is 2*d*V dimension.

Word2vec Derivations of Gradient

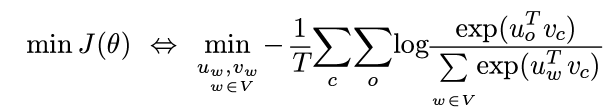
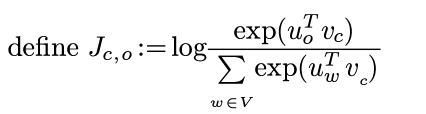
using chain rule and multi-var derivative:

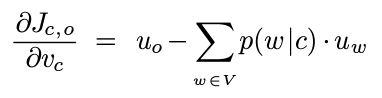
⇒ slope of the vector v_c w.r.t. J_c,o equals the current vector u_o minus the weighted average of context word u_w , i.e."expected context word".

Gensim Word Vector Visualization

gensim: word similarity package

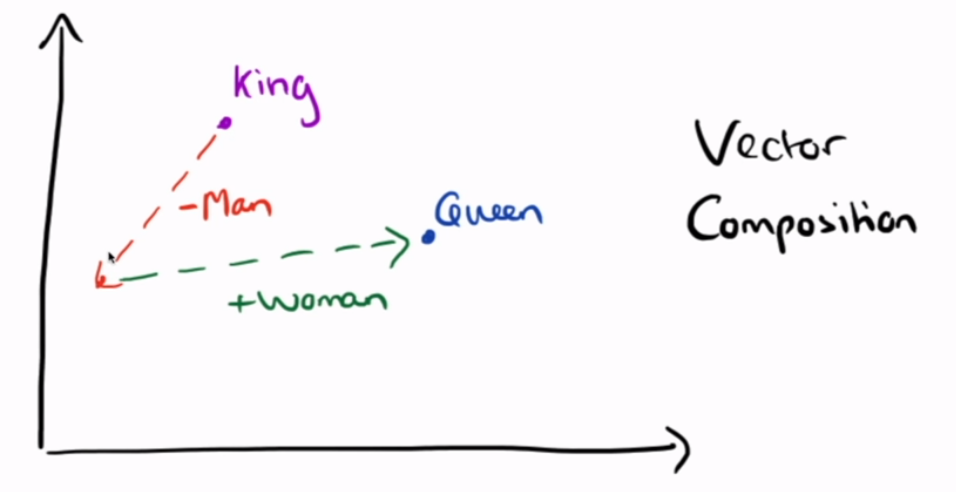
word composition