[Neural Networks and Deep Learning] week4. Deep Neural Network

Deep L-layer neural network

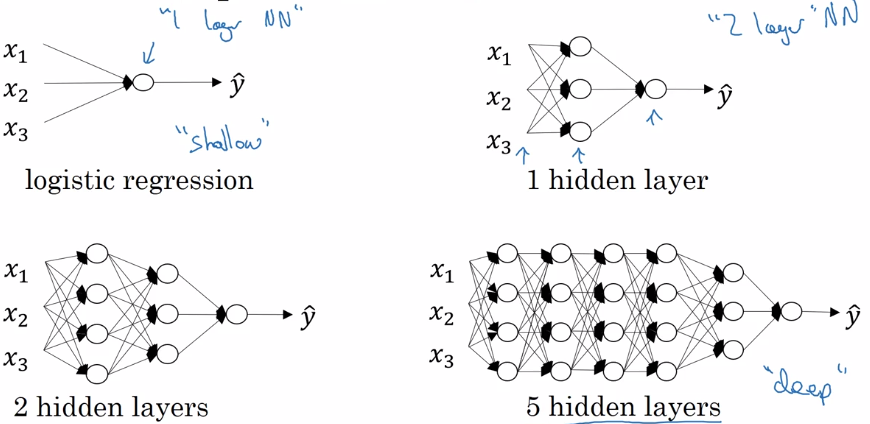
Layer counting:

• input layer is not counted as a layer, "layer 0"
• last layer (layer L, output layer) is counted.

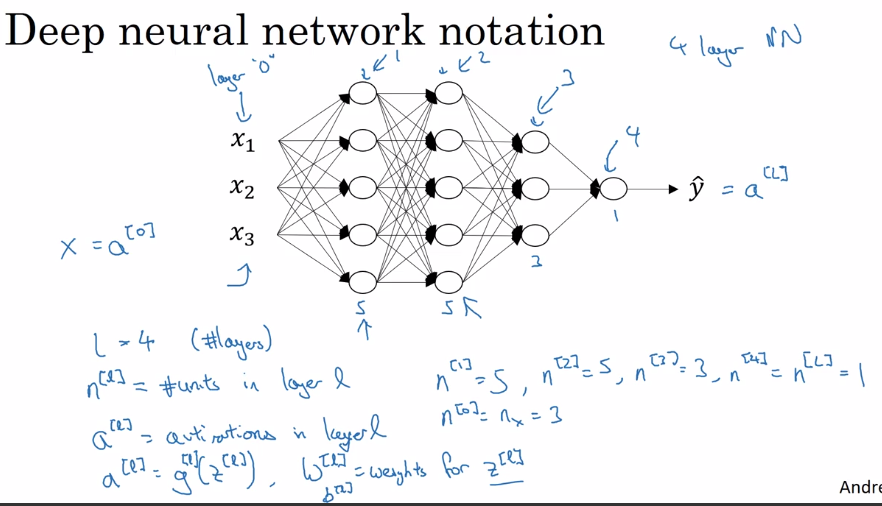
notation: layer 0 = input layer L = number of layers n^[l] = size of layer l a^[l] = activation of layer l = g[l]( z[l] ) → a[L] = yhat, a[0] = x

Forward Propagation in a Deep Network

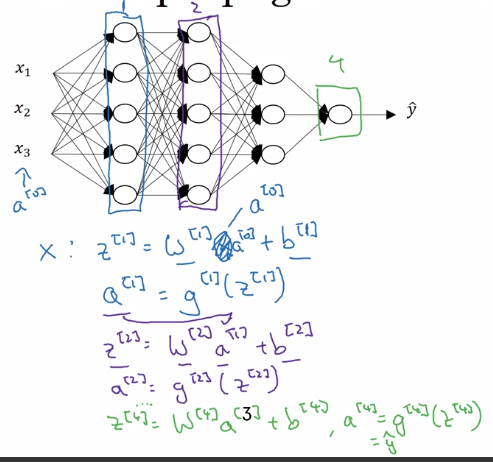
⇒ general rule:

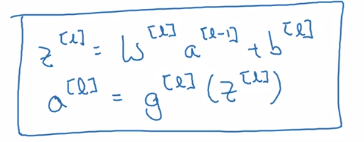
vectorization over all training examples: Z = [z(1),...,z(m)] one column per example ⇒

A[0] = X
for l = 1..L:
  Z[l] = W[l]A[l-1] + b[l]
  A[l] = g[l]( Z[l] )
Yhat = A[L]

Getting your matrix dimensions right

Debug: walk through matrix dimensions of NN, W[l].

Single training example dimension:
a[l-1].shape = (n[l-1], 1)
z[l].shape = (n[l], 1)
⇒ z[l] = W[l] * a[l-1] + b[l], shape = (n[l],1)
⇒ W[l].shape = (n[l], n[l-1]), b[l].shape = (n[l],1)

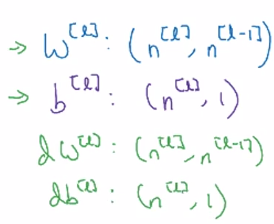
Vectorized (m examples) dimension:
Z = [z(1),...,z(m)] stacking columns.
Z[l].shape = (n[l], m)
Z[l] = W[l] * A[l-1] + b[l]

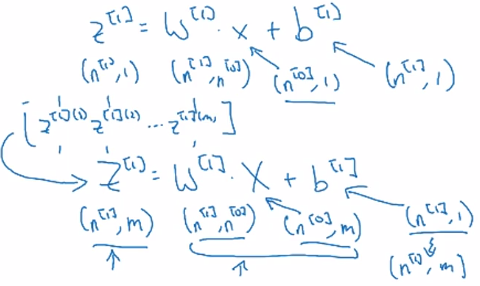
Z[l].shape = A[l].shape = (n[l], m)

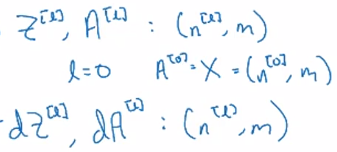
Why deep representations?

intuition:

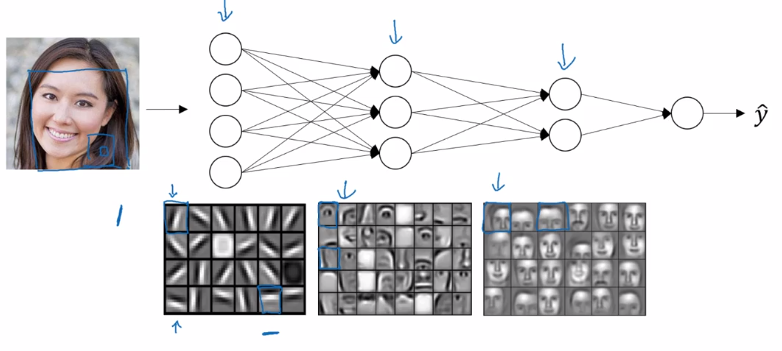
as layers grow: simple to complex representation / low to high level of abstraction.

Circuit theory: small deep NN is better than big shallow NN.

Example: representation of a XOR.join(x1..xn) function.

• Using deep NN ⇒ build an XOR binary tree

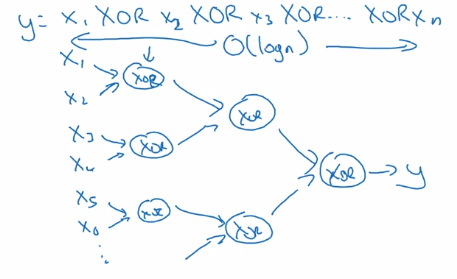
• Using shallow NN: one single layer → enumerate all 2^n configurations of inputs.

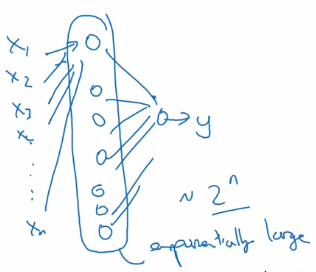
Building blocks of deep neural networks

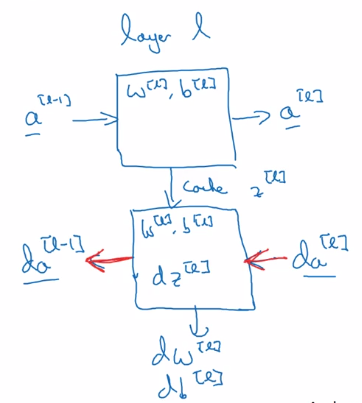
Fwdprop and backprop, for layer l.

• Fwdprop: from a[l-1] to a[l]

note: cache z[l] for backprop.

• Backprop: from da[l] to da[l-1], dw[l] and db[l]

Once the fwd and back functions are implemented, put layers together:

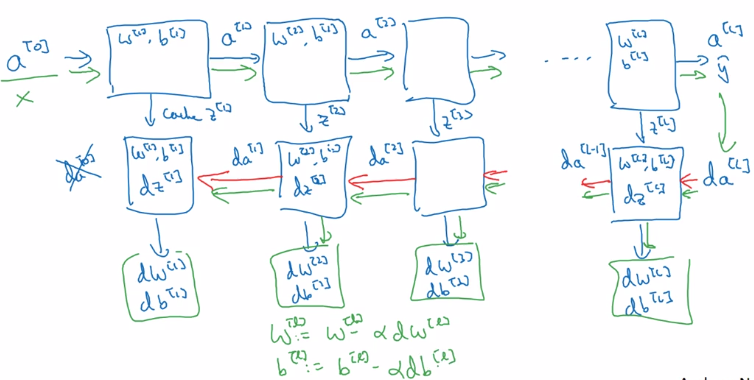
Forward and Backward Propagation

Fwd prop
input = a[l-1], output = a[l], cache = z[l]

Z[l] = W[l] * A[l-1] + b[l]
Z[l] = g[l]( Z[l] )

Back prop input = da[l], output = da[l-1], dW[1], db[l]

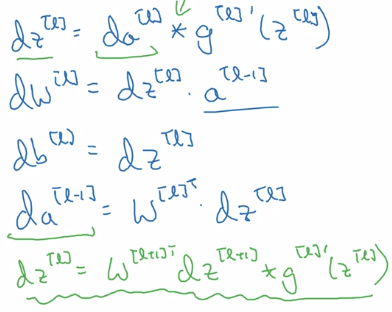
note:

• remember da = dL/da, so here da~='1/da' mathematically.
• derivate of matrix multiplication = transposed matrix derivative: (A*B)' = B^T' * A^T'
• initial paule of backprop: da[L] = dL/dyhat

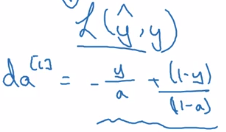
Vectorized version:

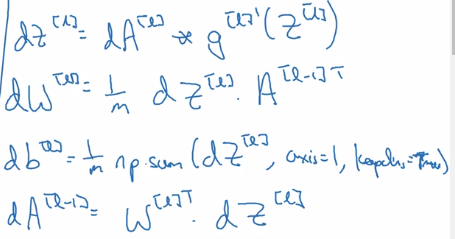
Parameters vs Hyperparameters

• parameters: W[l] and b[l] → trained from data
• hyperparams:
  • alpha (learning_rate), number of iterations, L, n[l] size of each layer, g[l] at each layer...
  • momentum, minibatch, regularization...

→ finally decides what params will be.

empirical: try out different hyperparams.

What does this have to do with the brain?

logistic regression unit ~~~> neuron in brain

assignment: implementing a L-layer NN

• params initialization:

note: different signature for np.random.randn and np.zeros:

W = np.random.randn(d0, d1) * 0.01
b = np.zeros((d0, d1)) # Needs putting dims in a tuple!

• function activation:

np.maximum is element-wise comparison, whereas np.max will apply on certain axis. so ReLU(x) = np.maximum(0, x)

• Fwd prop:

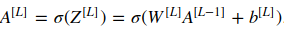
• cost:

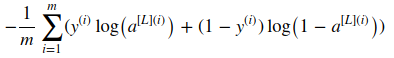
• backprop formula:

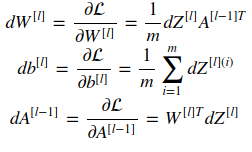
• initial paulse of backprop dA[L]:

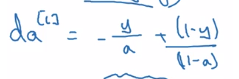
dAL = - (np.divide(Y, AL) - np.divide(1 - Y, 1 - AL))