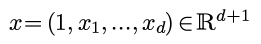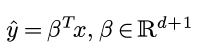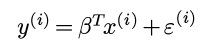[Algorithms II] Week 4-1 Tries

Sat, 05 Dec 2015 Category notes algorithm Series Part 7 of «Algorithms Princeton MOOC II»

More efficient version of symbol-table where the keys are strings.

1. R-way Tries

Two implementations of symbol tables that we've seen:

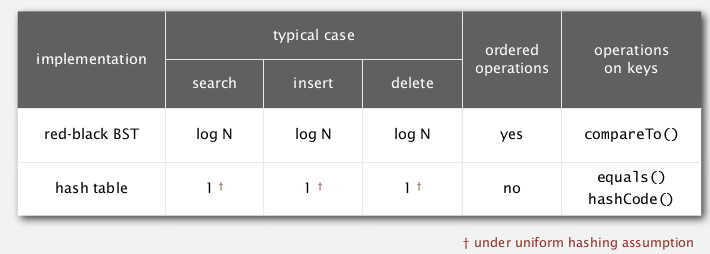
when keys are strings:
(L=string length, N=number of strings, R=radix)

for string keys ⇒ do better by avoiding examing the entire key.

goal: faster than hashtable, more …

[Algorithms II] Week 3-2 Radix Sorts

Mon, 23 Nov 2015 Category notes algorithm Series Part 6 of «Algorithms Princeton MOOC II»

This week: string sort.

1. Strings in Java

char data type

char in C

8-bit integer, 256 characters, 7-bit ASCII code

char in Java

16-bit Unicode

String data type

String: immutable sequence of characters
operations: lengthe, ith char, substring, concatenate

implementation: using a char[], maintain a length and an offset …

[Algorithms II] Week 3-1 Maximum Flow

Tue, 17 Nov 2015 Category notes algorithm Series Part 5 of «Algorithms Princeton MOOC II»

1. Introduction to Maxflow

Min-cut pb

input: edge-weighted digraph G, each edge e has weight("capacity") c[e]>=0, a source vertex s, a target vertex t.
def. an st-cut (A,B) is a partition of vertices into 2 disjoint sets A and B, with s in set A and …

[Algorithms II] Week 2-2 Shortest Paths

Sun, 15 Nov 2015 Category notes algorithm Series Part 4 of «Algorithms Princeton MOOC II»

1. Shortest Paths APIs

context: directe, weighted graphs.

shortest path variants

in terms of vertices:

source-sink: form one vertex to another
single source: from one vertex to all others (considered in this lecture)
all pairs

constraints on edge weights:

nonnegative weights
arbitary weights
eculidean

cycles:

no directed cycles
no negative …

[Algorithms II] Week 2-1 Minimum Spanning Trees

Wed, 11 Nov 2015 Category notes algorithm Series Part 3 of «Algorithms Princeton MOOC II»

1. Introduction to MSTs

Given: undirected connecte graph G with positive edge weights.
def. Spanning tree T
is a subgraph of G, that is both tree (connected, acyclic) and spanning(all vertices are included).

⇒ Goal: find a spanning tree with minimum weight sum.