This week: string sort.

1. Strings in Java

char data type

• char in C

8-bit integer, 256 characters, 7-bit ASCII code

• char in Java

16-bit Unicode

String data type

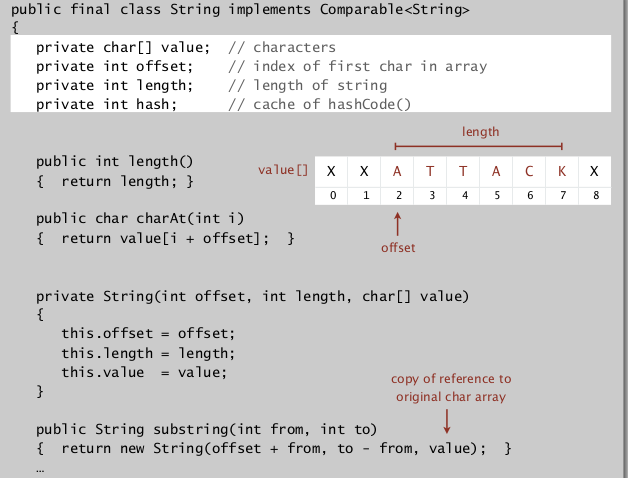
String: immutable sequence of characters
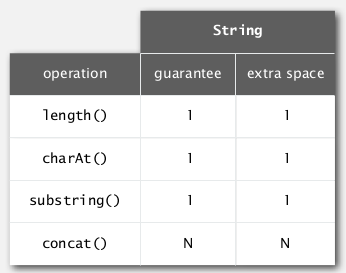
operations: lengthe, ith char, substring, concatenate

implementation: using a char[], maintain a length and an offset. ⇒ substring methode is O(1) time.

StringBuilder data type

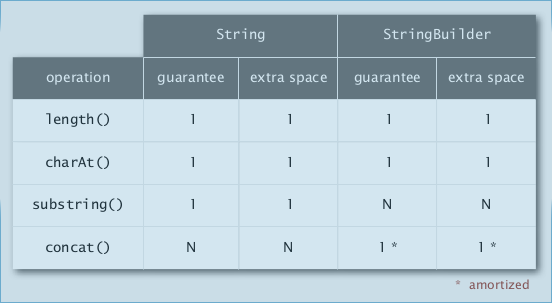
StringBuilder: mutable data type.
implementation: using a resizing char[] array (ArrayList).
⇒ contat in (amortized) constant time, substring in linear time!

ex.

• reverse a string: linear using StringBuilder, quad using String.
• form an array of suffixes: quad (time&space) using StringBuilder, linear (time&space) using String.

Longest Common Prefix:
runs in linear/subinear time ⇒ compareTo() for strings takes (sub)linear time!

Alphabet

alphabet different for different type of string (ex. binary numbers, DNA, ...)

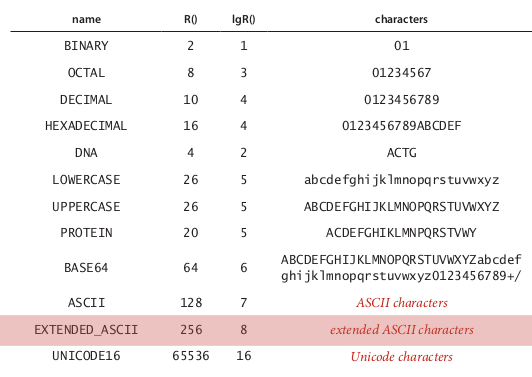
def. Radix R is number of digits in alphabet.

2. Key-Indexed Counting

review of compare-based sorting algorithms:

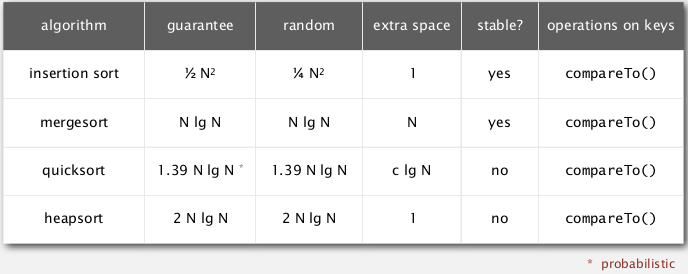
lower-bound for compare-based algorithms: ~NlgN (=Lg(N!))
⇒ goal: do better by avoiding using compares.

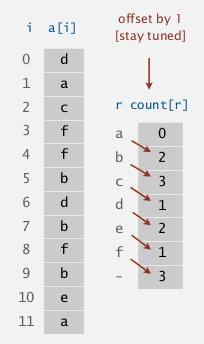
Key-indexed counting

is an algorithm to sort by character(ex. sort array of string by their 1st character).
Assumption: keys are integers between 0 and R-1 (<<N, small integer).
⇒ use keys as array index, to sort an array of N integers between 0 and R-1.

[algo]

• count freq of each key index (of size R+1)
• using count array, compute a cumulated freq (cumsum of count[])
• the cumsum[] array stores the index range of each key index:

index range of key-i in sorted array is [cumsum[i], cumsum[i+1]]

• then get the sorted array by going through the array and using cumsum[] array

⇒

public void keyIndexCounting(int[] a, int R){// entries in a[] are in range [0,R-1]  
    int N = a.length;  
    int[] count = new int[R+1]; // count[i] = freq of key i-1, count[0] = 0  
    for(int ai:a)   
        count[ai+1]++;  
    int[] cumsum = count; //cumsum = cumulated freq  
    for(int i=0;i<R;i++)   
        cumsum[i+1] += cumsum[i];  
    // the ranges of key i in sorted array should be [cumsum[i], cumsum[i+1]]  
    int[] aux = new int[N];  
    for(int ai:a)  
        aux[cumsum[ai]++] = ai;  
    a = aux;      
}

analysis

• running time: linear in time and in space.
• stable sorting: that's why we need the cumsum and aux array...

3. LSD Radix Sort

LSD = least significant digit (for string sorting)
(assume strings all of same length)
idea:

• consider chars from right to left
• sort using dth character as key (using key-indexed counting)

important: the key-indexed counting should be stable.

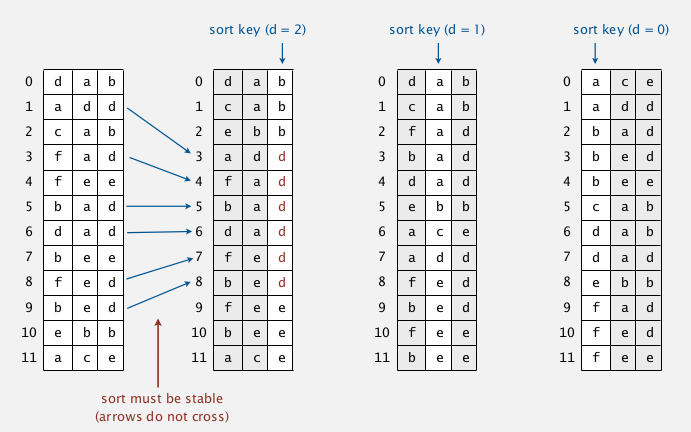
analysis

time: W * N (W=length of string)

correctness:
prop. LSD sorting works
pf. by induction on i
prove that: after pass i, strings are sorted by last i characters.

implementation

public static LSDsort(String[] a, int W){//W=fixed width  
    int R = 256;//for ASCII chars  
    int N = a.length;  
    String[] aux = new String[N];  
    for(int d=W-1;d>=0;d--){//W passes  
        //key-indexed counting at digit d  
        int count = new int[R+1];  
        for(String s:a)  
            count[s.charAt[d]+1]++;  
        for(int i=0;i<N;i++)  
            count[i+1] += count[i];//count = cumsum(count), range of each key  
        for(String s:a)  
            aux[s.charAt[d]++]=s;//put each key in right place  
        for(int i=0;i<n;i++)  
            a[i]=aux[i];  
    }  
}

• if keys are binary numbers → break into bit characters then apply LSD.
• if not fixed length → some fix..
• sort 1 million 32-bit integers? (Google/Obama interview) ⇒ LSD string sort~

4. MSD Radix Sort

most-significant-digit first (from left to right)
Idea.

• partition array into R pieces according to first character (the count[] array is the partition)
• recursively sort each subarrays

variable length: end-of-string are treated as before any char

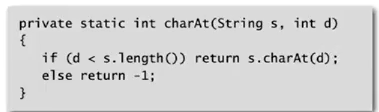
implementation

private static void sort(String[] a, String[] aux, int lo, int hi, int d){  
    if(hi<=lo) return;  
    //sort by dth character  
    int count = new int[R+2];// R+2 as we are taking account into the end-of-strings!!  
    for(int i=lo;i<=hi;i++) count[ a[i].charAt(d)+2 ]++;//charAt(end-of-string)=-1  
    for(int i=0;i<R;i++) count[i+1] += count[i]; //cumsum  
    for(int i=lo;i<=hi;i++) aux[count[a[i].charAt(d)+1]++] = a[i];  
    for(int i=lo;i<=hi;i++) a[i] = aux[i-lo];// attention: aux is filled from index 0 instead of lo  
    //recursively sort each subarray (R subarrays in total, ranges stored in count[])  
    for(int r=0;r<R;r++)  
        sort(a, aux,lo+count[r], lo+count[r+1]-1, d+1);  
}

analysis

• can recycle aux[], but not count[].
• too slow for small subarrays (if len(subarray)<<R)
• huge nb of subarrays because of recursion

improvement ⇒ cutoff to insertion sort...

characteristics of MSD sort:
examines just enough chars to sort.
→ can be sublinear in N.

MSD vs. quicksort

disadvantages for MSD:

• random access of memory (cache inefficient)
• too many instructions in inner loop
• extra space for count[]
• extra space for aux[]

disadvantages for qsort:

• NlgN nb of string compares
• has to rescan many chars for keys with long prefix matches

5. 3-way Radix Quicksort

⇒ combine benefits of qsort and MSD.

idea: do 3-way partition by the dth character.

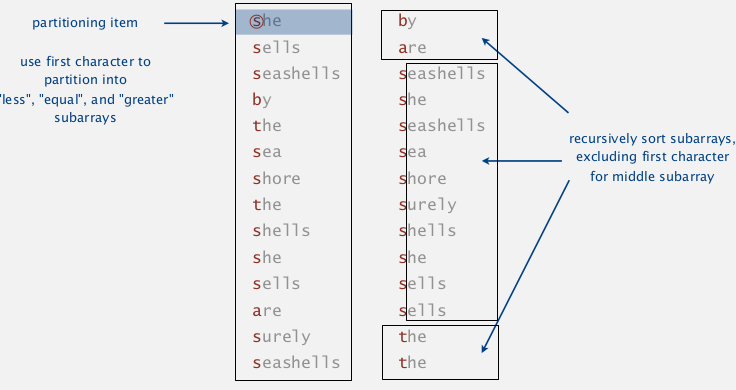
• less overhead than R-way partitioning for MSD
• do not re-examine chars equal to the partitioning char

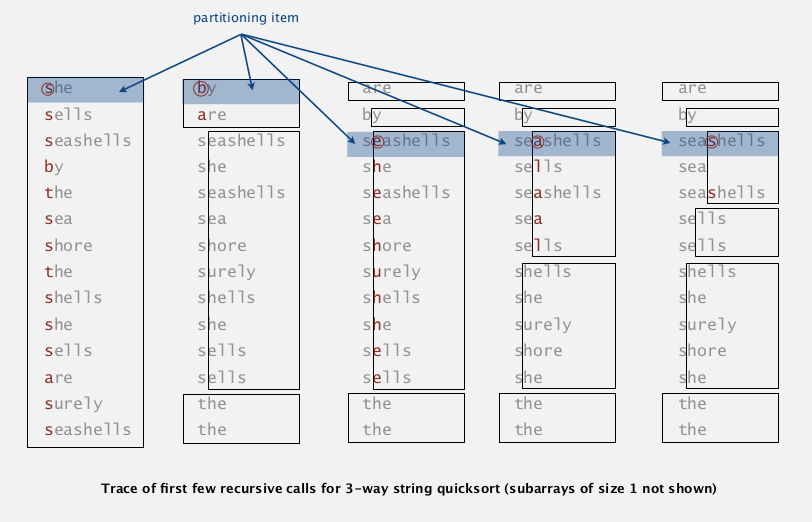
Implementation

modification of the 3-way qsort.

private static sort(String[] a, int lo, int hi, int d){  
    if(hi<=lo) return;  
    int lt = lo, gt = hi, i=lo+1;// use 3 pointers: lt, i, gt  
    char pivot = a[lo].charAt(d);  
    while(i<=gt){//invariant: a[lo,lt)<pivot, a(gt,hi]>pivot, a[lt,i]=pivot  
        char c = a[i].charAt[d];  
        if(c<pivot) exch(a,lt++,i++);  
        else if(c>pivot) exch(a,i,gt--);  
        else: i++;  
    }//3-way partition  
    sort(a,lo,lt-1,d);  
    if(pivot>=0) sort(a,lt,gt,d+1);//pivot<0 means end-of-string  
    sort(a,gt+1,hi,d);  
}

analysis

wrt. qsort:

• from NlgN string compares to NlgN char compares.
• avoids re-comparing long common prefixes.

wrt. MSD:

• short inner loop
• cache friendly
• in-place

6. Suffix Arrays

(some applications of suffix array)

keyword-in-context search

given N chars (N huge), preprocess it to enable fast substring search.
⇒ suffix sort

• generate suffix array (linear time & space )
• sort on the suffix ⇒ brings repeated suffixes together

longest repeated substring

• brute force algorithm

try all i, j as starts of indices, then compute longest common prefix (LCP)
→ O(D*N2) where D is length of longest repeated substring.

• ⇒ use suffix array

sorting suffix array will bring repeated substrings together
java code:

//int lcp(String s1, String s2) defined  
public static lrs(String s){  
    int N = s.length;  
    String[] suffix = new String[N];  
    for(int i=0;i<N;i++) suffix[i] = s.substring(i);//construct suffix array  
    Arrays.sort(suffix);// sort suffix array ==> using 3-way radix sort   
    // one pass to get longest repeated substring (bigest lcp)  
    String lrs = "";  
    for(int i=0;i<N-1;i++){  
        int lcp = lcp(suffix[i], suffix[i+1]);  
        if(lcp>lrs.length) lrs = suffix[i].substring(0, lcp);  
    }  
    return lrs;  
}

lrs worst-case input: lrs very long (say N/2).
⇒ quadratic for lrs and for sorting.

→ improvement of lrs for worst-case performance:
Manber-Myers algo
sketch:

• phase 0: sort suffix[] on 1st char
• phase i: given suffix[] is sorted based on first 2^(i-1) chars → create suffix[] sorted on first 2^i chars.

each phase: double the nb of chars sorted on.
maintain an inverse[] array, to make comparisons constant time.
performance: NlgN

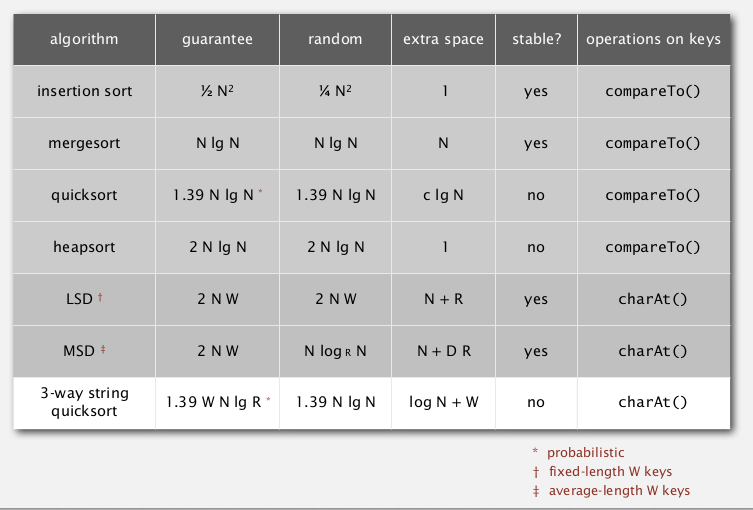
String sorting summery

• can have linear sort: use chars as array index
• sublinear sort: not all date need to be examined
• 3-way radix qsort is asymptotically optimal