1. Intro to graphs

Graph: vertices connected by edges.

terminology:

• path: sequence of vertices connected by edges
• cycle: path with same starting and ending vertex
• two vertices are connected: if there is a path between

ex of graph problems:

• path: or connectivity
• shortest path
• cycle
• Euler tour (ouii..)
• Hamilton tour
• MST
• bi-connectivity: is there a vertex whose removal disconnects the graph?
• planarity
• isomorphism

2. Graph API

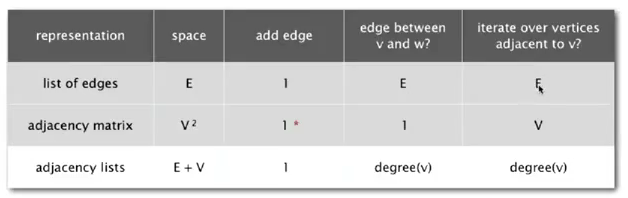
graph representation

• vertex representation: use integers between 0 and V-1
• anormalies: self-loop and multiple edges are possible

  public class Graph{   
      Graph(int V);   
      void addEdge(int v, int w);   
      Iterable<Integer> adj(int v);   
      int V();// nb of vertices   
      int E();// nb of edges   
  }
  

print all edges:

basic functions:

static int degree(Graph g, int v){   
    int deg = 0;   
    for(int w:G.adj(v)) deg++;   
    return deg;   
}   
static int nbOfSelfloops(Graph g){   
    int cnt = 0;   
    for(int v=0; v<G.V(); v++)   
        for(int w:G.adj(v))    
            if (w==v) cnt++;   
    return cnt/2;   
}

edge representation

• set-of-edge implementation: a list of all edges ⇒ can lead to inefficient implementation
• adj-matrix implementation: maintain a 2d (V*V) boolean array ⇒ space complexity too heavy
• adj-list implementation: vertex-indexed array, each array entry is a Bag (类似桶bucket) ⇒ sutable for sparse graphs

adj-list implementation:

private final int V;   
private Bag<Integer>[] adj;   
public Graph(int V){   
    this.V = V;   
    this.adj = (Bag<Integer>[]) new Bag[V];// java cannot create generic array   
    for(int v = 0; v<V; v++) adj[v] = new Bag<Integer>();   
}   
public addEdge(int v, int w){   
    adj[v].add(w);   
    adj[w].add(v);// if undirected graph   
}

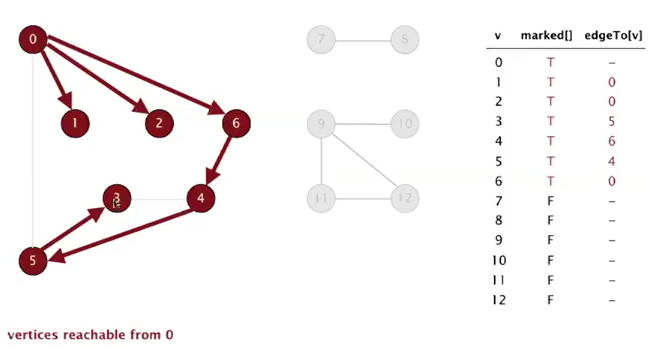
3. Depth-First Search

Tremaux maze exploration: trace back when no unvisited vertices availiable.
动画好看...
DFS goal: systematically search through a graph.
design pattern: decouple graph data and graph processing.

public class Paths{   
    Path(Graph G, int s);// graph G and source s   
    boolean hasPathTo(int v);   
    Iterable<Integer> pathTo(int v);   
}

algo:

注意每次访问节点以前就将其mark.

implementation

• 用一个boolean数组visited[]作为标记
• 为了找到一条具体的路径(ie, 一系列节点), 维护一个prev[]数组, 存放当前节点是从哪个节点走过来的.

//public class DFSpaths extends Paths...   
boolean[] visited = new boolean[V];   
int[] prev = new int[V];   
public void dfs(int v){   
    visited[v] = true;   
    for(int w: G.adj())   
        if(!visited[w]) {   
            prev[w]=v;   
            dfs(w);   
        }   
}   
public Iterable<Integer> pathTo(int v){   
    Stack<Integer> s = new Stack<Integer>();   
    for(int x = v; x!=s; x = prev[x])    
        s.push(x);   
    return s;   
}

properties

prop.
DFS visite all edges in time propotional to the sum of their degrees(ie. nb of edges).

4. Breadth-First Search

not recursive algo.
maintain a queue, add to queue for all vertices not-marked.

implementation

• use visited[] to mark vertices
• use a prev[] array to get explicit path
• use a dist[] array to record the shortest dist from v to source (can use dist to replace visited)

  public void bfs(Graph G, int s){   
      boolean visited[] = new boolean[G.V()];   
      int prev[] = new int[G.V()];   
      int dist[] = new int[G.V()];   
      Queue<Integer> q = new Queue<Integer>();   
      visited[s] = true;   
      q.push(s);   
      while(!q.isEmpty()){   
          int v = q.dequeue();   
          for(int w:G.adj(v))   
              if(!visited[w]) {   
                  prev[w] = v;   
                  visited[w] = true;   
                  q.enqueue(w);   
              }      
      }   
  }
  

property

prop.
BFS computes the shortest path from s to all vertices using time propotional to E+V.

intuition: BFS examines nodes by increasing distance

5. Connected Components

dealing with connectivity(equivalence) queries ⇒ answer in constant time (with preprocessing).

public class CC{   
    boolean connected(int v, int w);   
    int count();// nb of CCs   
    int id(int v);//id for a CC   
}

⇒ Union-Find ? ⇒ Use DFS!!

def. connected component is a maximal set of connected vertices.

algo: for each unmarked vertex, run dfs(with increasing cc id)...
after the preprocessing, we can get the array id[] and cc count cnt...

6. Graph Challenges

some typical pbs
pb1. bipartite graph

Can we divide vertices into 2 subsets, where all edge go from one subset to other.
⇒ can be done with dfs. cf. booksite

pb2. cycle detection
⇒ simple using dfs.

pb3. Euler cycle
Find a cycle that uses all edges exactely once.
[Euler] a graph is Eulerian iff all vertices have even degree.
⇒ typical diligent algo students can do. cf. booksite

pb4. Hamilton cycle
Find cycle that visits each vertex exactly once.
⇒ intractable (typical NP-complete pb)

pb5. isomorphism of graphs
Are two graphs identical except for vertex names?
⇒ no one knows...

pb6. planary graph
Lay out a graph in the plane without crossing edges?
⇒ expert level. exists linear time algo based on DFS by Tarjan, but too complicated.