2. notes
  3. [Algorithms II] Week 4-1 Tries

[Algorithms II] Week 4-1 Tries

Category notes algorithm Series Part 7 of «Algorithms Princeton MOOC II»
目录

More efficient version of symbol-table where the keys are strings.

1. R-way Tries

Two implementations of symbol tables that we've seen:

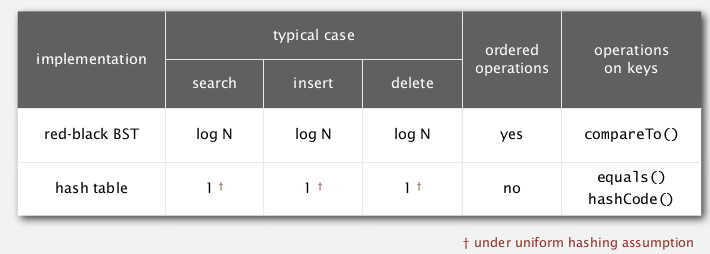
when keys are strings:
(L=string length, N=number of strings, R=radix)

for string keys ⇒ do better by avoiding examing the entire key.

goal: faster than hashtable, more flexible than BST !

String Symbol Table API

public class StringST<V>{// implements ST<String, V>  
    public void put(String key, V val);  
    public V get(String key);  
    public void delete(String key);  
}

R-way tries

A trie is a tree where:

  • except the root, each node store characters (instead of string keys) — in fact the chars are stored in links
  • each node has R children
  • store value in node if the node corresponds to the last char in key.

example: (a trie)

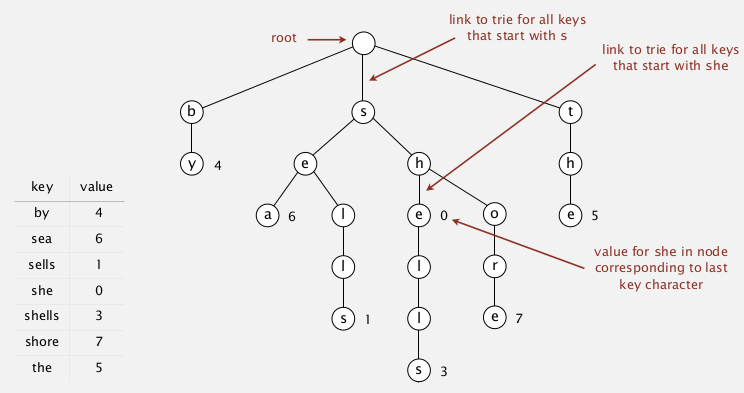
  • search in a trie get()

hit if when search ends the node has a non-null value
miss if reach a null link or have null value when search ends.

  • insertion in a trie put()

follow the links as the chars indicate in the key
→ if meet null links: create new node
→ when reach last char in key: set the value of the node

Java implementation

trie node class:
in each node use an array of size R to store links... 

private static class Node{  
    private Object val;// because cannot create arries of generic type (array of Node)  
    private Node[] next = new Node[R];// chars are implicitly defined by link index  
}

另外关于为什么内部类Node声明为static, 参考这里:
http://www.geeksforgeeks.org/static-class-in-java/

implementation: use private recursive methods, 和BST的实现类似, 定义一个递归的private函数, 返回插入后的Node, 很有用. 

public class TrieST<Value> {  
    pirvate final int R = 256; // ASCII chars  
    private Node root = new Node();  
    private static class Node{  
        private Object val;// because cannot create arries of generic type (array of Node)  
        private Node[] next = new Node[R];// chars are implicitly defined by link index  
    }  
    public void put(String key, Value val){  
        this.put(root, key, val, 0);// use private recursive helper method  
    }  
    private Node put(Node x, String key, Value val, int d){  
        // `d` is the index of char to put  
        // returns the inserted node

        if (x==null) x = new Node();  
        if (key.length()==d) x.val = val;  
        else{  
            char c = key.charAt(d);

            x.next[c] = put(x.next[c], key, val, d+1);  
        }  
        return x;  
    }  
    public boolean contains(String key){return get(key)!=null;}  
    public Value get(String key){  
        Node nd = this.get(root, key, 0);  
        if(nd==null) return null;  
        return (Value) x.val; // cast back  
    }  
    private Node get(Node x, String key, int d){  
        // returns the node that contains val for key  
        if(x==null) return null;  
        if(d==key.length()) return x;  
        char c = key.charAt(d);

        else return get(x.next[c], key, d+1);  
    }  
}

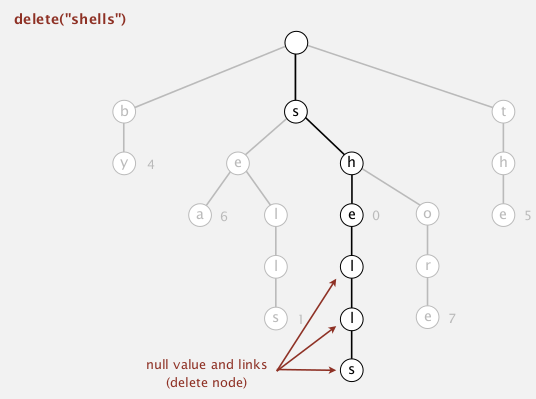
delete node in trie:

  • find the node and set the val to null
  • if a node has 0 links(leaf) and val==null: delete it and recursivly go up.

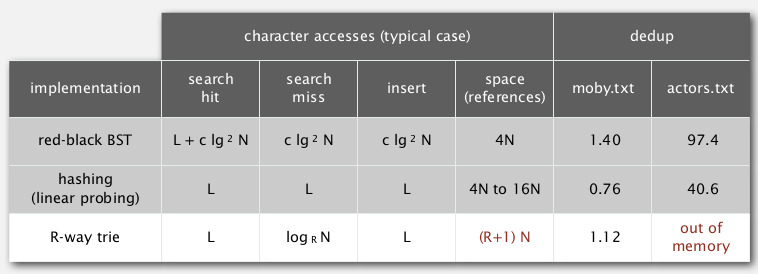
analysis

time:
search hit — L nodes examined.
serach miss — sublinear in L
space:
each node has R links (possibly null) — too much memory for large R !

Application
interview question: data structure for spell checking.

2. Ternary Search Tries

Solution to the memory issue of R-way tries — much fewer null links. ternery=tuple of 3...
TST:

  • store chars (and vals) explicitly in nodes
  • each node has 3 children:
    • smaller, larger: TST that starts with char smaller/bigger than its char c.
    • equal: the TST with keys that starts with this char c
    • (所以除了用smaller/larger连接的节点在Rway trie里属于同一层


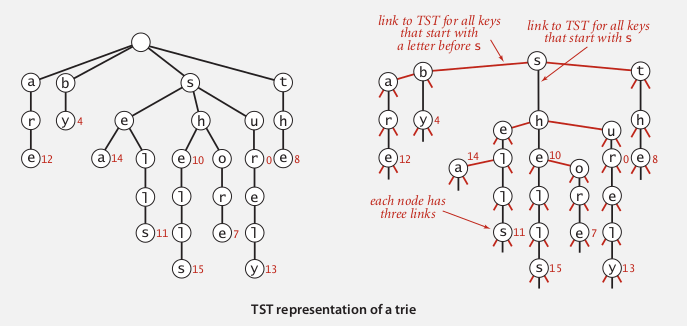
类似于3-way radix sort(同一篇paper里提出的), 有有点RBTree的意思...

searching in TST: quite similar to BST search, will go down ("equal" or "middle") when the current node matchs current char...

Implementation

Node class: 

private class Node{  
    private Value val;  
    private char c;// store char explicitly  
    private Node left, mid, right;  
}

TST class (again use recursive helper functions)
有一种写BST代码的感觉, 另外由于这次char是显式存在node里, 代码反而更好理解了... 

public class TST<Value>{  
    private class Node{...};  
    private Node root;  
    public void put(String key, Value val){  
        this.put(root, key, val, 0);  
    }  
    private Node put(Node x, String key, Value val, int d){  
        char c = key.charAt(d);// char to process  
        if(x==null) x = new Node(c);  
        if(c==x.c) {  
            if(d==key.length()-1) x.val = val;  
            else x.mid = put(x.mid, key, val, d+1);// d+1 means we go down one level  
        }  
        else if (c<x.c) x.left = put(x.left, key, val, d);// do not increment if the current char is not matchd  
        else x.right = put(x.right, key, val, d);  
        return x;  
    }  
    public Value get(String key){  
        Node nd = this.get(root, key, 0);  
        if(nd==null) return null;  
        return nd.val;  
    }  
    private Node get(Node x, String key, int d){  
        if(x==null) return null;  
        char c = key.charAt(d);  
        if(x.c==c) {  
            if(d==key.length()-1) return x;  
            else return get(x.mid, key, d+1);  
        }  
        else if(c<x.c) return get(x.left, key, d);  
        else return get(x.right, d);  
    }  
}

Hybrid of TST and Rway trie

  • at root: do R^2 branching
  • other nodes are TSTs

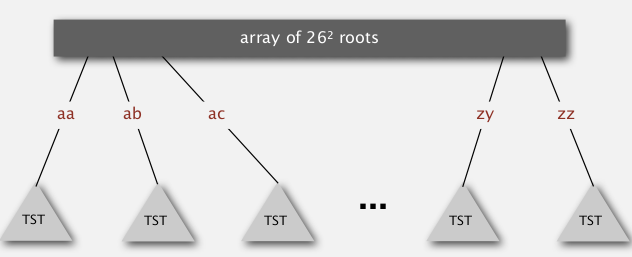
analysis

space cost: linear in N.
time: if keys arrive in rand order... (can use rotation to get worst-case guarantee..)

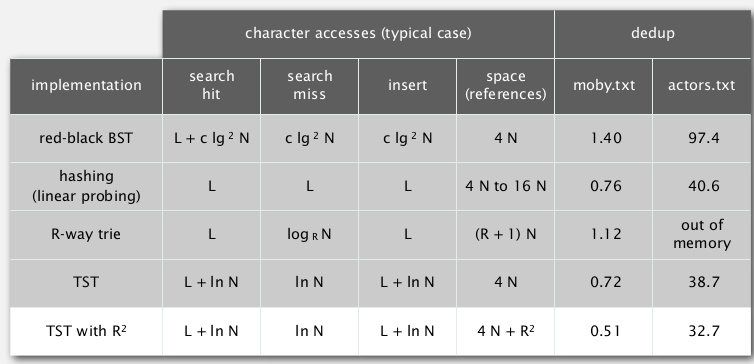
Hashing vs. TST

Hashing:

  • need to check entire key no matter hit or miss
  • performance relies on hash functions
  • donot support ordered operations

TST:

  • examines just enough chars
  • support ordered operations

3. Character-Based Operations

some very useful char-based operations:

  • prefix match
  • wildcard match: use a dot to represent any char
  • longest prefix: find the key that is the longest prefix of a string

API

public class TrieST<Value>{  
    // functions decalred before..  
    Iterable<String> keys;  
    Iterable<String> keysWithPrefix(String s);  
    Iterable<String> keysThatMatch(String s);  
    Iterable<String> longestPrefixOf(String s);
}

keys(): ordered iteration

keys(): just an inorder-traversal of the Rway trie →dfs, + maintain the chars in the path (root to current node). 

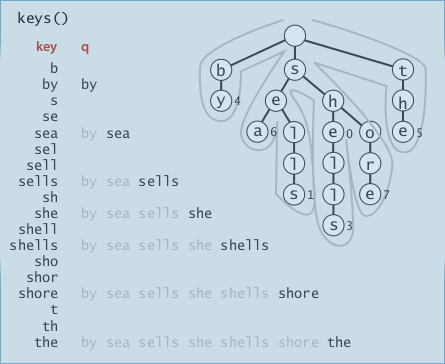
public Iterable<String> keys(){  
    Queue<String> q = new Queue<String>();  
    collect(root, "", q);// helper fcn  
    return q;  
}  
private void collect(Node x, String pathstr, Queue q){  
    if(x==null) return;  
    if(x.val!=null)// if this is a key  
        q.enqueue(pathstr);// pathstr is the string of chars from root to x  
    for(char c=0;c<R;c++) // dfs  
        collect(x.next[c], pathstr+c, q);  
}

prefix match

very useful: ex. autocomplete, search bar, ...
implementation⇒ just find the end of that prefix, then call keys() on the subtrie.
之前写的俩helper function这里发挥作用了: 

public Iterable<String> keysWithPrefix(String prefix){  
    Node subtrieRoot = get(root, prefix, 0);  
    Queue<String> q = new Queue<String>();  
    collect(subtrieRoot, prefix, q);  
    return q;  
}

longest prefix

⇒ just do a search and keep track of the longest key that we encounterd. 

public String longestPrefixOf(String s){  
    int len = search(root, s, 0, 0);  
    return s.substring(0, len);  
}  
private int search(Node x, String s, int d, int len){  
    if(x==null) return len;  
    if(x.val!=null) len=d;// this is the current longest prefix  
    if(d==s.length()) return length;   
    char c = s.charAt(d);  
    return search(x.next[c], s, d+1, len);  
}

application: T9 texting

classique... G面试以及X的TP里都有涉及过...

  • first: generate all string combinations
  • second: call get() on the trie of dictionaries.

Other Variants

Patricia trie

improvement: remove the one-eay branching (put >1 chars in a node).

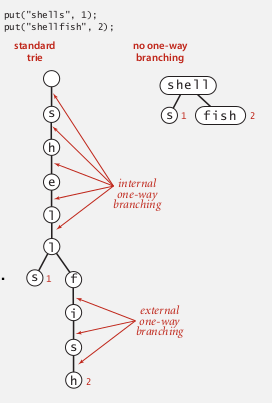
suffix tree

  • patricia tree of the suffix
  • linear time construction
  • ongest repeated substring, longest common substring, longest palindromic substring, substring search, tandem repeats... 好有用!!...

Summery

comments powered by Disqus