Goal: classify problems according to computational requirements.
bad new: for huge number of pbs we don't know...

1. Introduction to Reductions

shifing gears:

• from individual problems to problem-solving models.
• from linear/quard to polynomial/exponential pbs
• from implementation details to conceptual framwork

suppose we could (not) solve pb X efficiently
⇒ what else pbs could (not) we solve efficiently ?

def. reduction
Pb X reduces to pb Y if you can use an algo that solves Y to solve X.

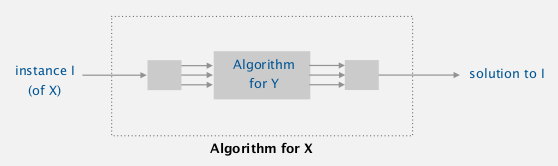
for an instance of pb X → transform it into an instance of pb Y → translate the solution for Y to solution for X.

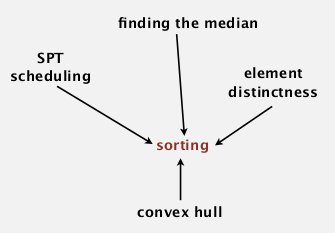
ex1. finding median can reduce to sorting... cost = NlogN+1
ex1. element distinctness can reduce to sorting... cost = NlogN + N

2. Designing Algorithms

algo design: by reduction to problems that we know how to solve (sorting/shortest path/flow/...)

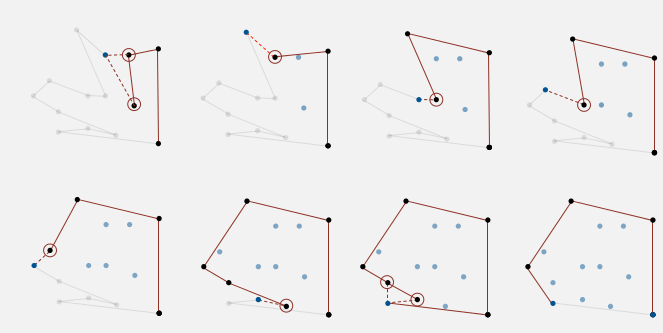
ex1. convex hull reduces to sorting

Gram scan algo... (discussed in algo-I course)
cost = NlogN + N
algo. Gram scan

• pick a point with smallest y-coord
• sort all points by polar angle wrt the picked point
• consider points in this order, discard points that creates clockwise turn

ex2. undirected shortest path (nonneg weights) reduces to directed shortest path

cost: ElogV + E
algo. replace each undir-edge by 2 dir-edge...

3. Establishing Lower Bounds

goal: prove that a pb requires (at least) a certain nb of steps.

ex. any compare-based sorting requires NlogN compares. log(N!) = NlogN

Bad news: very hard to estibalish lower bounds.
Good new: can spread the lower bound NlogN by reducing to sorting (if cost of reduction is small).

def. linear-time reduction
pb X linear-time reduces to pb Y if X can be solved with:
1. linear nb of op for reduction
2. constant nb of calles to Y

ex. almost all reductions we've seen so far...

ex. proof of lower bound for convex hull

prop. sorting linear-time reduces to convex hull
(注意这次是反向的! )
pf.
for an instance of sorting: x1 ... xn
⇒ convert to convex hull instance: (x1, x1^2), ... , (xn, xn^2)

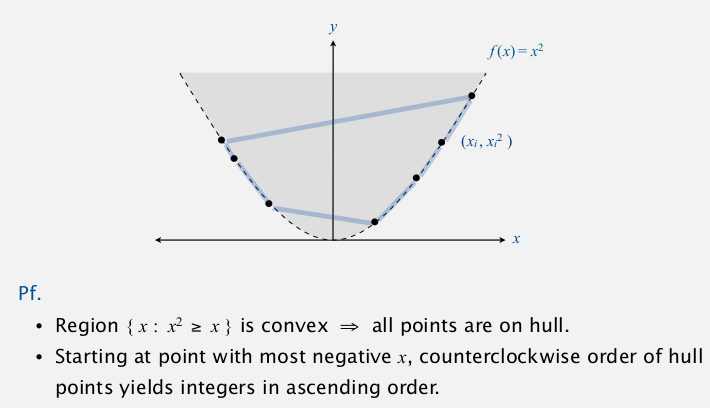
⇒ implication: all (ccw-based) convex hull algo cannot be easier than NlgN ! (otherwise sorting would be easier..)

lesson: Establishing lower bounds through reduction is an important tool in guiding algorithm design efforts.

4. Classifying Problems

prove that pb X and pb Y have the same complexity:

• show X linear-time reduces to Y
• show Y linear-time reduces to X
• conclude that X Y have the same complexity (even if we don't know what it is)

ex. sorting and convex hull...
一个囧囧的脑洞:

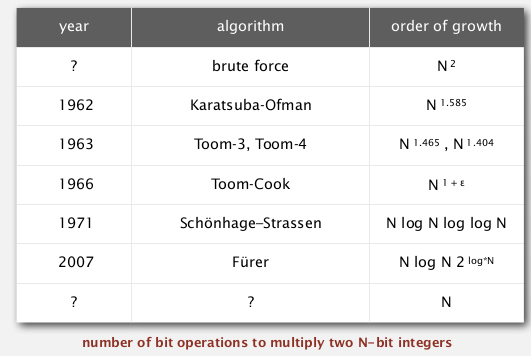
ex. integer arithmetic reductions: integer multiplication

integer multiplication: of two N-bit integers.
Its complexity (unknown) is denoted as M(N)
brute force: N^2 ops → so M(N) = Omega(N2)
many other integer ops can reduce to integer multiplication:

what is M(N)?

ex. linear-algebra reductions: matrix multiplication

compute product of 2 N*N matrices.
Its complexity (unknown) is denoted as MM(N)
brute force: N^3
operations that can reduce to matrix-multiplication:

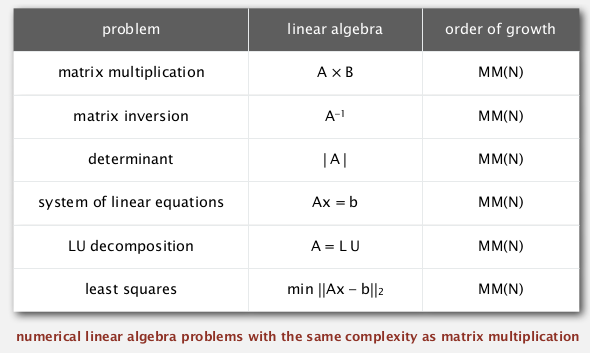
what is MM(N)?

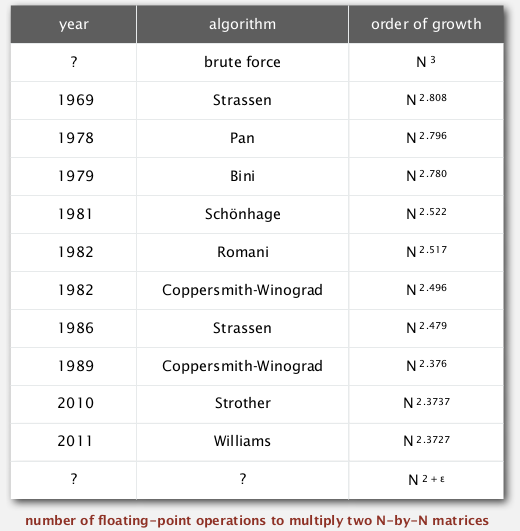
summary