Here is a mindmap of the common algorithms and data structures, it can give an overview of the algorithmic terms.

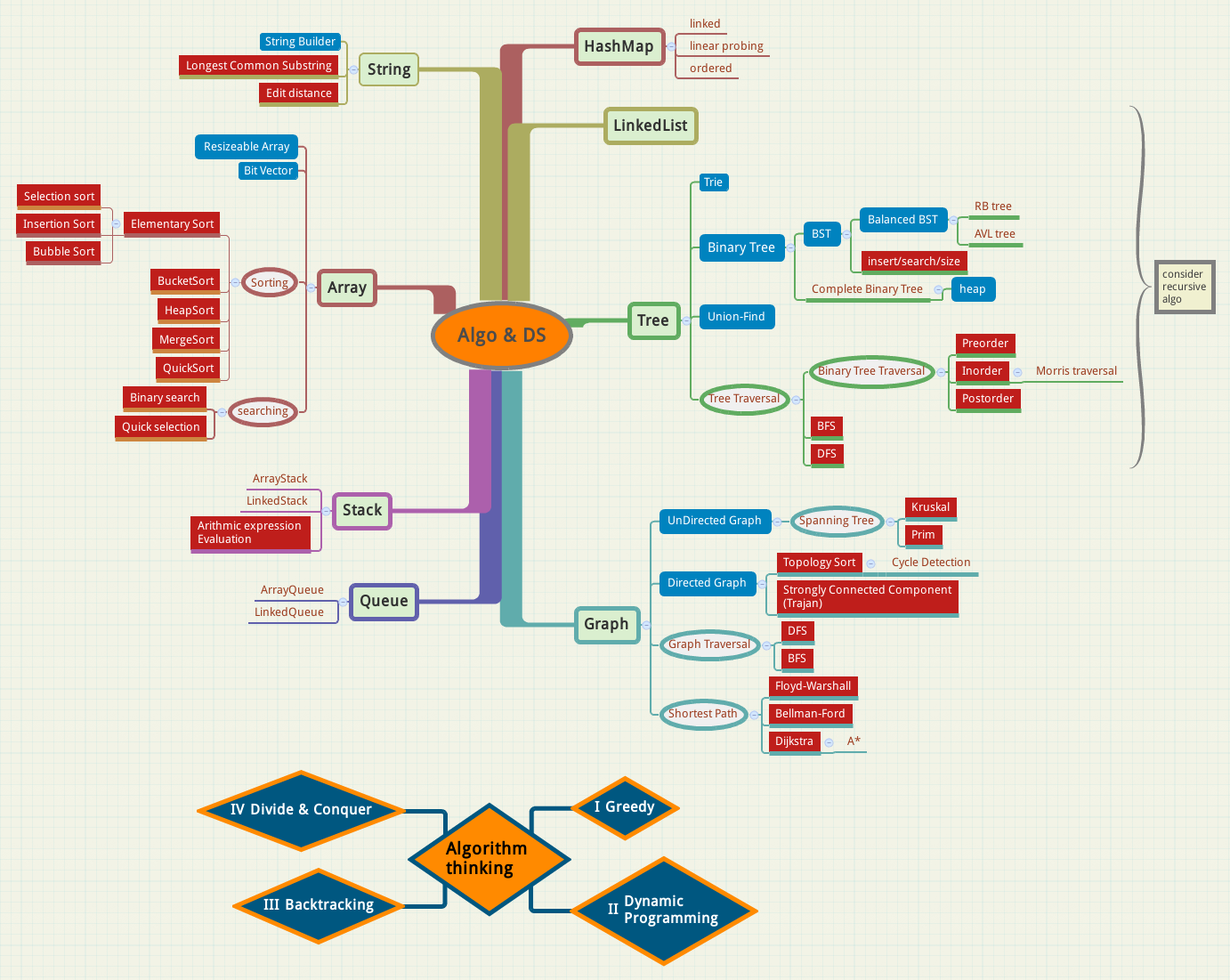
I shall update its content later on. And maybe write some blog entries on some of the items.

This mindmap is drawn using xmind.

Can we do better than BST if we do not need ordered operations ?

(No compare methods, use equals method)

Idea: save items in an array.
Hash function: method for calclulating the array index of a key.

Issues:

• computing hash function
• equality tests
• collision resolution

Classic space-time tradeoff.

1. Hash Functions ...

1. 1d Range Search

Goal: intersections of geometric objects.

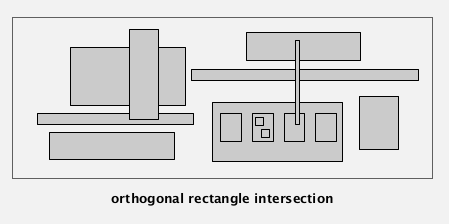
Solution: BST

1d range search

operations required:

• insert
• search
• delete
• range search: all keys between k1 and k2
• range count: how many keys are between k1 and k2

→ find points on an interval

implementation by BST

range count
using the rank ...

goal: lgN for insert/search/delete operations (not necessarily binary trees..)
3 algo: 2-3 tree, (left leaning) red-black tree, B-tree

1. 2-3 Search Trees

def. 2-3 tree

• allow 1 or 2 keys per node, & 2 or 3 children per node:
  • 2-node: one key, 2 children (ordinary BST node)
  • 3-node: 2 ...

(BST是锻炼递归代码的好题目)

1. Binary Search Trees

def. BST
A binary tree where each node has a key:
for every node, the key is larger than all nodes in left subtree, smaller than all nodes in right subtree.

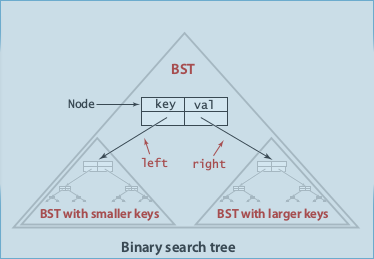
Fields: key, val, left, right

Implementation

An inner class of BST nodes:

private class ...

1. Symbol Table API

key-value pair abstraction

• insert a value with a key
• given a key, search for its value

Association array abstraction

Associate a value to a key — generalized array: a[key]=val.

public class ST<Key, Value>{   
    void put(Key k, Value v);//remove key if value=null ...

1. API and elementary implementations

Collection: data struct for inserting and deleting items (ex. stack and queue).
Priority queue: a special kind of collection — remove largest/smallest element.

API:

public class Max<Kye implements Comparable<Key>>{   
    public MaxPQ();    
    public void insert(Key k);   
    public Key delMax();    
    public boolean isEmpty();     
    public ...

(maybe best algorithm for sorting.)

1. Quicksort

Idea:

1. shuffle the array
2. Partition the array into two subarrays to left and right of pivot (*now pivot is *in its final position)

no larger entry to the left of pivot
no smaller entry to the right of pivot

1. sort each subarray recursively ...

Two classical sorting algorithms: mergesort, quicksort.

1. Mergesort

Divide and conquer: top 10 algorithms of the 20th century, invented by von Neumann.

Idea:

• divide array into 2 halves
• recursively sort each half
• merge two sorted halves

Implementation

Merge:
Goal: a[lo] to a[mid] and a[mid+1] to a ...

1. Introduction

rearanging array of size N into ascending order
test client code: Insertion.sort(a);

sort any datatype

callback

callback = reference to executable code
i.e. passing functions as argument to sort() method
sort() function calls object's compareTo() method

→ implement the Comparable interface:

    public class XX implements Comparable ...