(maybe best algorithm for sorting.)

1. Quicksort

Idea:

1. shuffle the array
2. Partition the array into two subarrays to left and right of pivot (now pivot is in its final position)

no larger entry to the left of pivot
no smaller entry to the right of pivot

1. sort each subarray recursively

Implemetation

The partition process:
这个方法也比较巧妙.
Use 2 pointers i and j (个人觉得用hi, lo, pivot更好...) :

→ a[i]>=a[lo], a[j]<=a[lo] (注意是大于等于/小于等于)
⇒ exchange i and j
→ Scan until i and j cross (ie. j<=i)
⇒ finally exchange lo with j
函数的签名定义的好: 把lo到hi部分的数组分成两部分, 并返回分割点的index.

private static int partition(Comparable[] a, int lo, int hi){   
    int i=lo+1, j=hi;   
    while(i<j){   
        while( i<=hi && less(a[i],a[lo]) ) i++; //a[i]>=a[lo]   
        while( j>=lo && less(a[lo],a[j]) ) j--; //a[j]<=a[lo]   
        if(i<j) exch(a,i++,j--);   
    }   
    exch(a,lo,j); //exchange pivot with j   
    return j; //j in its final position   
}

这个函数其实并不好写对:

• test for cross pointers is not trival (ex. edge case: the pivot is the smallest/largest entry in the range)
• i<=hi is necessary !
• for keys equal to a[lo]: better to stop at them

invariance:

**Quicksort: **
使用partition函数和辅助sort函数(recursive). 注意在整个流程开始以前先shuffle一下.

private static void sort(Comparable[] a, int lo, int hi){   
    if(hi<=lo) return;   
    int pivot = partition(a, lo, hi);   
    sort(a,lo,pivot-1);   
    sort(a,pivot+1,hi);   
    return;
}   
public static void sort(Comparable[] a){   
    StdRandom.shuffle(a); // don't forget to shuffle the array   
    sort(a,0,a.length-1);   
}

The randomness is preserved: the subarrays after partitionning is still randomly ordered.

Analysis

Performance: ~40% faster than mergesort.

Best case

compares = NlgN

(each partition will divide the array in half)

**Worst case **

compares = 1/2*N^2

N+(N-1)+...+1
if the array is already in order, each partition will have one subarray of length=0

**Average case **

proposition **
On average, for array with N distinct keys, the #compares = ~2NlnN, #exchanges = ~1/2NlnN.
Proof.*
C(N) := # compares for N entries
pivot 在N个数离的排名是uniform的
接下来的数学推到很漂亮(不过可能没啥用..)

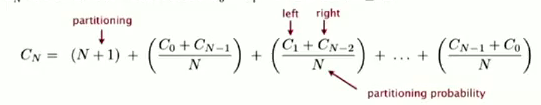
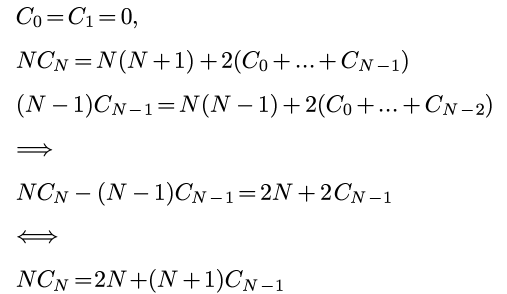
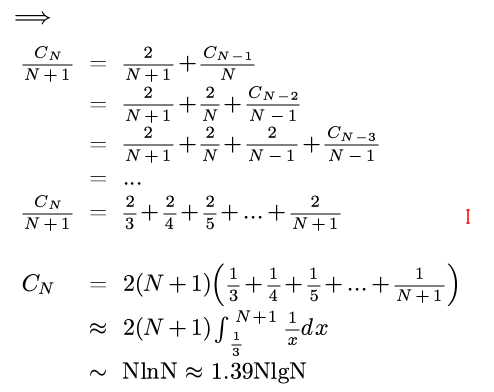
(上面最后一行写错了... 是2NlnN...orz) random shuffle: probalistic guarantee against worst case.

Pitfalls **
implementations will get quadratic performance if array:

• is sorted or reverse sorted
• has many duplicates (even if randomized)

Staility **
Quicksort is NOT** stable.
partitionning can make long range exchanges

Practical improvements

• cutoff to insertion sort for <10 items

→ ~20% improvement
Or we can leave the small subarrays unsorted and sort them at last using insertion sort

• estimate median by sampling 3 items

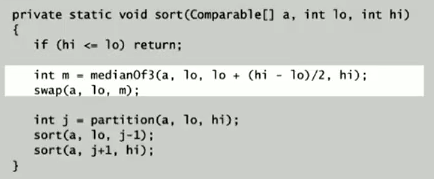
→ 10% improvement

2. Selection

Goal: given un array, find the kth largest item.

• Upper bound for this problem: NlgN (just sort the array)
• for small k (ex k=1,2,3), the upper bound is N (one-pass/two-pass)
• Lower bound is N: at least have to look at everything

Quick select

Algo proposed also by Hoare:

1. partition the array into two arrays left of pivot and right of pivot.
2. if pivot==k: return
3. continue the partition for just one of the subarrays

类似于二分查找的过程....
注意这里是不用递归的! 因为partition函数返回的直接就是pivot在整个数组里的位置!

Implementation

privater static int partition(Comparable[] a, int lo, int hi){...}

public static Comparable select(Comparable[] a, int k){   
    StdRandom.shuffle(a);   
    int lo=0,hi=a.length-1;   
    while(true){   
        int j = partition(a,lo,hi);   
        if(j<k) lo=j+1;   
        if(j==k) return a[j];   
        else hi=j-1;   
        if(hi<=lo) break;   
    }   
    return a[k];//这里不太理解为什么会在hi<lo的时候直接返回a[k]   
}

Analysis

Proposition **
Quick selection takes linear* time on average.
proof *
intuitively, each partition will ct the subarray size in half:
N+N/2+N/4+... = 2N
formal analysis 略...

worst case: quadratic (but very rare to happen)

Theoretical results

3. Duplicate keys

if array contains many duplicate keys.

• huge array
• small number of distinct keys

**for mergesort **
insensitive... always ~NlgN compares.

for quicksort **
Will get quadratic time if not stop on equal keys. (found in 1990s)
mistake: put all items equal to pivot *to just one side *
→ N^2 compares if all keys are equal from lo to hi.
correct: put all items equal to pivot in their final place.

3-way partitionning

(by Dijkstra)
partition the array into 3 parts:

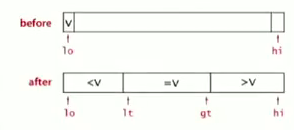
Dijkstra's 3-way partition algo:
使用3个指针: lt指向中间部分的左边界, gt指向右边界; i指针从左向右扫描, 算法很subtle:

• lt=lo, gt=hi, i=lo
• if a[i]==v : i++
• if a[i]<v: exch(i,lt), i++, lt++
• if a[i]>v: exch(i,gt), gt--
• repeat until i and gt cross (i>gt)

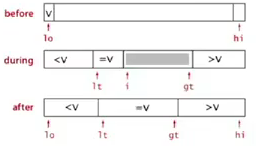
invariance:

• [lo, lt) all < v
• [lt, i) all == v
• (gt, hi] all >v

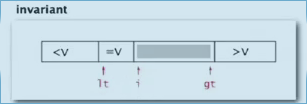
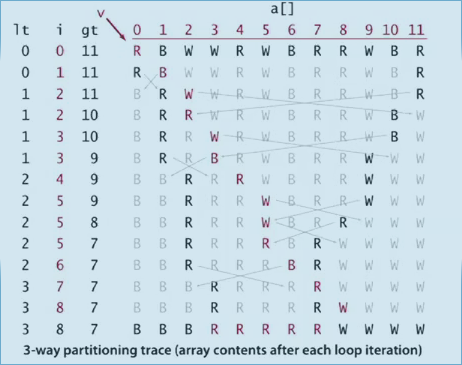
Implementation: 3-way quick sort

不必再写partition函数, 直接在sort递归函数里面.

private static void sort(Comparable[] a, int lo, int hi){   
    if(hi<=lo) return; // 递归函数别忘了先写终止条件...   
    int lt=lo, gt = hi;   
    Comparable v = a[lo];   
    for(int i=lo;i<=gt;){ //不能写 i++   
        if( less(a[i],v) )   
            exch(a, i++, lt++);   
        else if ( less(v,a[i]) )   
            exch(a,i,gt--);   
        else // v==a[i]   
            i++;   
    }   
    sort(a, lo, lt-1);   
    sort(a, gt+1, hi);  
}

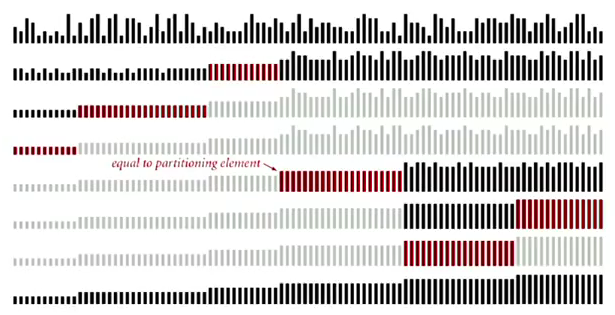
当N个数有很多重复的时候, lower bound可以变小于NlgN:

And Sedgewick proved that the 3-wy partition is propotional to the lower bound....

4. System Sorts

Arrays.sort() in java:

import java.util.Arrays;

quicksort for primitive arrays, mergesort for objects: java设计者认为如果用obj array表示空间不是问题...

Pb in java's system sort: killer input exsit (havn't shuffle)...

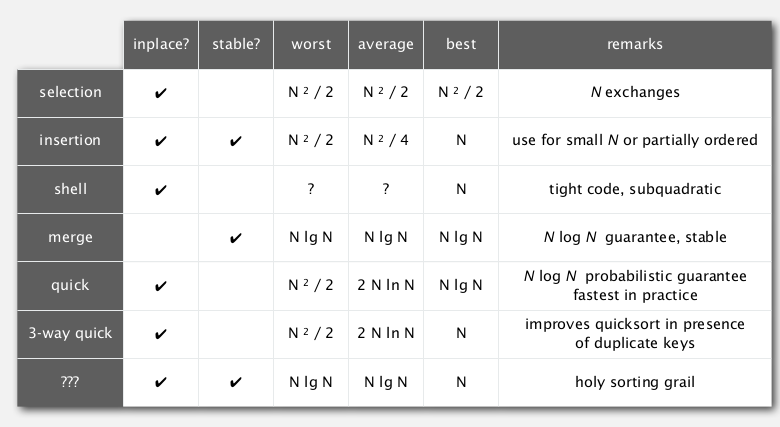
总结一下学过的5/6种排序: