Can we do better than BST if we do not need ordered operations ?
(No compare methods, use equals method)
Idea: save items in an array.
Hash function: method for calclulating the array index of a key.
Issues:
- computing hash function
- equality tests
- collision resolution
Classic space-time tradeoff.
1. Hash Functions
Goal: scramble the keys uniformly to produce a table index.
- effcient to compute
- all indices are equally likely for any key
challenge: need different approach for different key types.
Java's hashing
All java object has a methode int hashCode()
requirement:
- if x.equals(y) ⇒ x.hashCode()==y.hashCode()
-
(hopefully) if x.equals(y)==false ⇒ x.hashCode!=y.hashCode()
-
Default implementation: memory address for x.
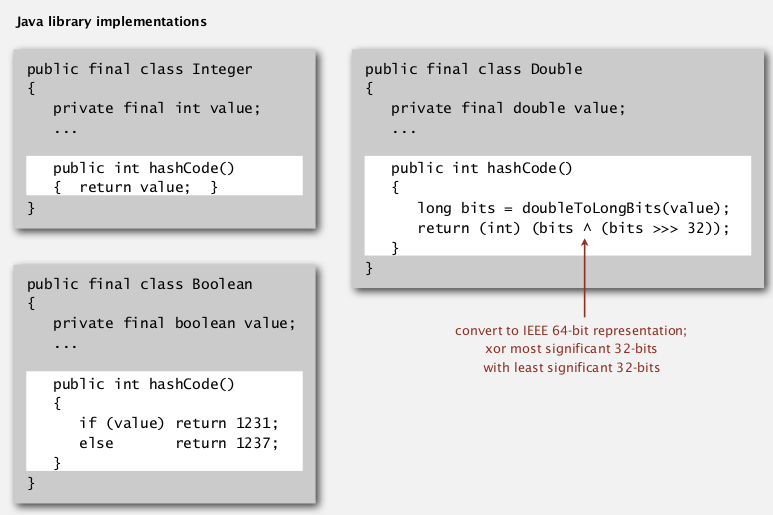
- Custom implementations for standard types: Integer, Double, String, File, URL, Date...
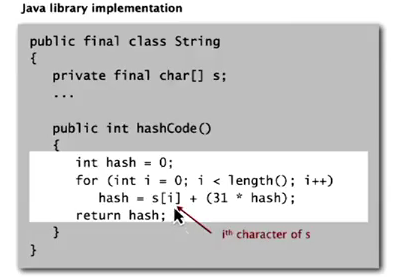
Strings: Horner's method — compute a polynome.
recipe for user-defined types:

Modeular hasing
(hash code VS hash function)
- Hash code: 32-bit integer between -2^31 and 2^31-1 (can be negative!!)
- Hash function: integer between 0 and M-1 (used directly as array index, should >=0)
BUG code:
private int hash(Key k){
return k.hashCode()%M;
}
→ bug: number returned can be negative !
1-in-billion bug code:
return Math.abs(k.hashCode()) % M;
→ bug: Math.abs() returns negative numbers for -2^31
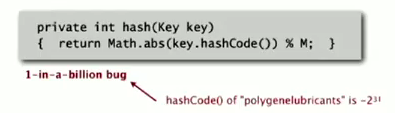
correct code:
just take the first 31 bits: x&0x7fffffff
return k.hashCode()&0x7fffffff % M;
另一个hash的思路是用random(用hashcode作为随机种子)
uniform hasing assumption
each key is equally likely to hash to an integer between 0 and M-1
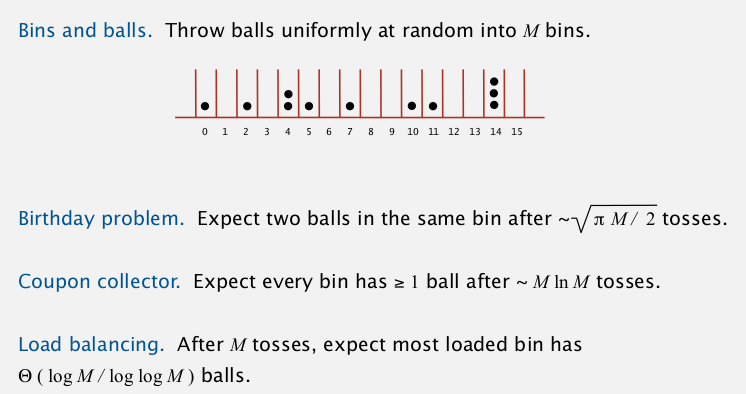
一些数学结论:
2. Separate Chaining
one strategy for collision resolution.

idea: Using a table of size M < N, build a list for each of the table positions.
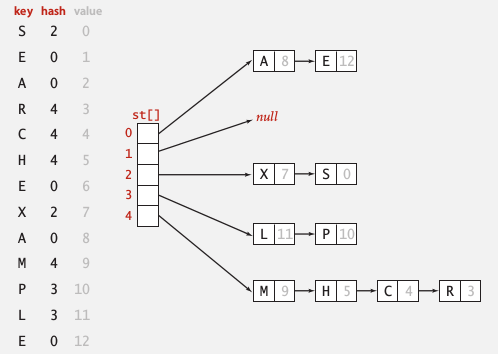
implementation
public class SeparateChainingHashST<Key, Value>{
private int M = 97;
private Node[] st = new Node[97];
private static class Node{
Object key, val; // no generic array creation!
Node next;
public Node(Key k, Value v, Node nxt){...}
}
int hash(Key k){
return (k.hashCode()&0x7fffffff) % M;
}
public Value get(Key k){
int h = hash(k);
for(Node x=st[h]; x!=null; x=x.next)
if(k.equals(x.val)) return (Value)x.val; //cast
return null;
}
public void put(Key k, Value v){
int h = hash(k);
for(Node x=st[h]; x!=null; x=x.next)
if(k.equals(x.val))
{x.val = v; return;}
st[h] = new Node(k,v,st[h]);
}
}
注意内部类Node里用的是Object — 因为不能声明generic array.
analysis
proposition
Under the assumption of uniform hashing, the number of keys in a list is within a constant factor to N/M.
proof.
binominal distribution.
M times faster than sequential search
→ typical choice: M ~ N/5
3. Linear Probing
Another approch for collision resolution.
idea: open addressing
Use an array of size M>N, when a key collides, find next open slot.

- insert: when occupied, move pointer until got open slot
- search: when not found, move pointer until find or reach open slot
- delete: set key to null, then for all items behind this key: set to null, then insert this key......
array M must be larger than N ⇒ array resizing is necessary.
implementation
public class LinearProbingHashST<Key, Value>{
private int M, N;
private Object[] keys;//cannot use generic array
private Object[] vals;
public void put(Key k, Value v){
int i = hash(k);
for(;keys[i]!=null;i=(i+1)%M)
if(keys[i].equals(k))
{vals[i]=v; return;}
keys[i]=k;
vals[i]=v;
}
public Value get(Key k){
int h=hash(k);
for(;keys[h]!=null;h=(h+1)%M)
if(k.equals(keys[h])) return (Value)vals[h];//ugly cast
return null;
}
}
cluster
def. cluster
A contiguous block of items.
New keys are more likely to hash into a cluster.
Knuth parking pb:


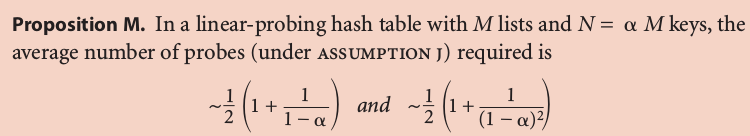
(当年Knuth就是在证明了这个以后决定写那套书)
Typical choice: N/M ~ 1/2 (3/2 for search hit and 5/2 for search miss)
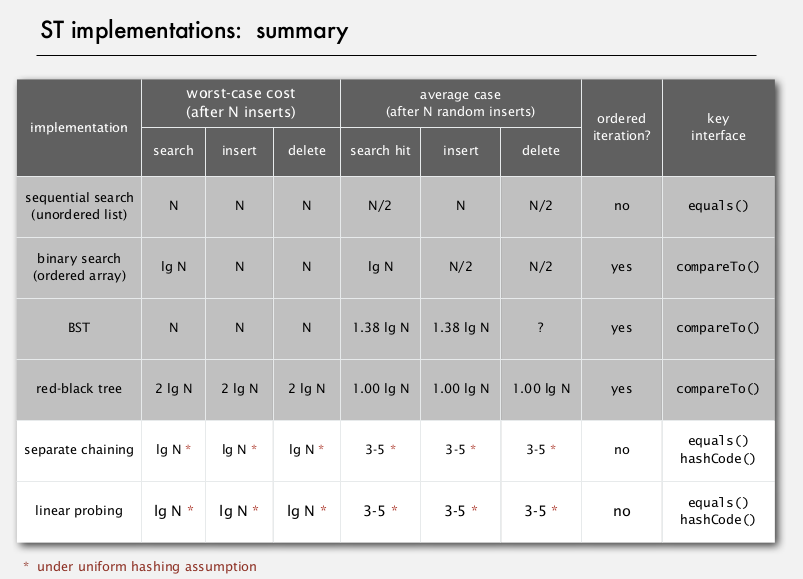
4. Hash Table Context
widely used in applicataions.
cost for computing hash VS cost for searching:
hashCode() for strings in java 1.1: exemain only 8-9 evenly spaced characters to save time.

uniform hashing assumption: performance not guaranteed...


one-way hash functions
Hard to find a key that hash to a desired value, or 2 keys having the same hash value.
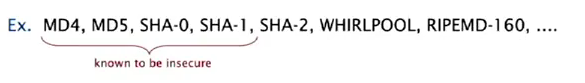
used for fingurprints or store passwords, but too expensive for ST implementations.
Seperate chaining VS linear probing

variations

ST choice: hash tables VS balanced search trees

Part 13 of series «Algorithms Princeton MOOC I»:
- [Algorithms I] Week 1-1 Union-Find
- [Algorithms I] Week 1-2 Analysis of Algorithms
- [Algorithms I] Week1-Lab: Percolation
- [Algorithms I] Week 2-1 Stacks and Queues
- [Algorithms I] Week 2-2 Elementary Sorts
- [Algorithms I] Week 3-1 Mergesort
- [Algorithms I] Week 3-2 Quicksort
- [Algorithms I] Week 4-1 Priority Queue
- [Algorithms I] Week 4-2a Elementry Symbol Tables
- [Algorithms I] Week 4-2b Binary Search Trees
- [Algorithms I] Week 5-1 Balanced Search Trees
- [Algorithms I] Week 5-2 Geometric Applications of BSTs
- [Algorithms I] Week 6 Hash Tables
Disqus 留言