1. Dynamic Connectivity pb

pb statement

a set of N obj, indexed by 0,1,...,N-1 ⇒ UNION: connect objects void union(int p, int q) FIND: is there a path connecting 2 obj? boolean connected(int p, int q)

ex:

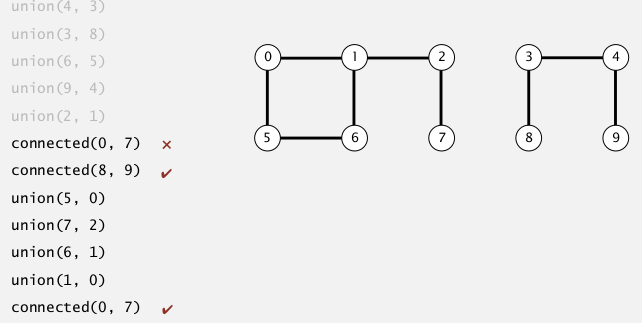
connect components(联通分支): max set of obj that are mutually connected.

UF API

• union(p,q): connect 2 obj
• connected(p,q): test if p and q are connected
• find(p): find the component id of p
• count(): nb of components

注意: 命名不是很好, 这里的find()函数不对应FIND query, connected()函数才是真正的FIND query, find()函数是为了connected()函数而做的一个辅助函数(find(p): return the root of the node p ) 在connected里就可以调用find: return find(p)==find(q)

应该是interface更好一些...

public interface UF{
void union(int p, int q);
boolean connected(int p, int q);
//int find(int p);
//int count();
}

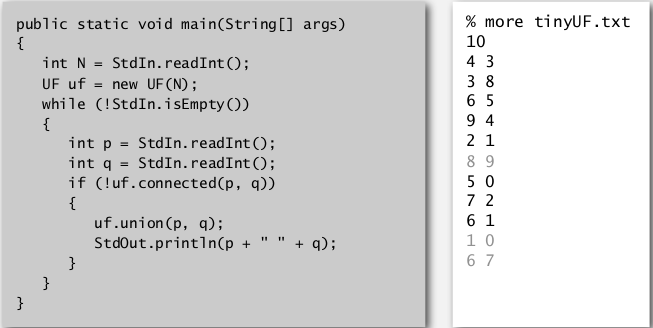
测试client:

2. Quick Find

"eager approach"

data structure

⇒ an int array id[] initialized to id[p]=p for all p interpretation: id[p] = component id of obj p ⇒ p and q are connected iff* id[p]==id[q] (ie. find very fast) 没有用find()函数

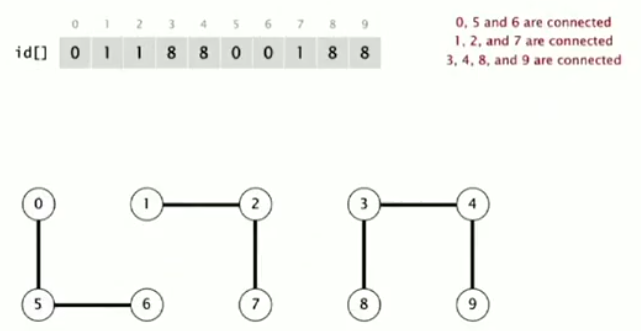
UF operations

• FIND:

connected(p,q): very fast, just check id[p] and id[q]

• UNION:

when merging 2 components : union(p,q): id[p]=id[q](总是让第一个参数p的id变为第二个参数q的id),
⇒ then have to modify all entries with id equal to id[p] !
⇒ too many entries to change

implementation

(class QuickFindUF implements UF)

complexity:

• FIND: cte
• UNION: lin...

if N obj + N unions ⇒ quad time !
btw, 程序运行速度: ~10^9/s

3. Quick Union

"lazy approach"

data structure

⇒ also an int array id[] considering a set of trees, 此时每个联通分支都是一个tree
interpretation: id[p] = parent index of obj p (觉得这个数组叫做father更好....)
⇒ p is a root node iff id[p]==p

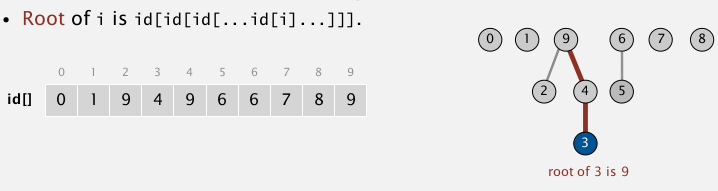
UF operations

• FIND:

connected(p,q):check if root of p == root of q

• UNION:

union(p,q):just set p's root to be child of q's root (把第一个参数p的那棵树放入第二个参数q的树的根节点作为子树)

• root():

前两个的操作都需要一个函数查找一个节点的root, 需要写一个函数实现, 也很简单, 一路找parent即可:

private int root(int p){
    while (p!=id[p]) p=id[p];
    return p;
}

implementation

complexity

in the worst case (all elements is in a list form), root() is ~N, so:

• FIND: lin
• UNION: lin

quick find和quick union的问题:

4. Quick Union Improvements

improvement1: weighting

keep track of tree size ⇒ balance by taking the small tree be a child of the large tree

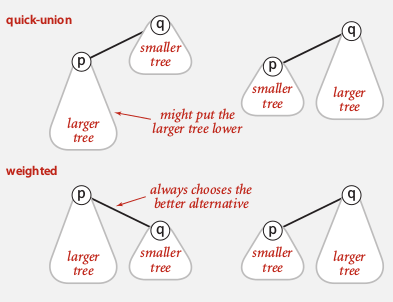
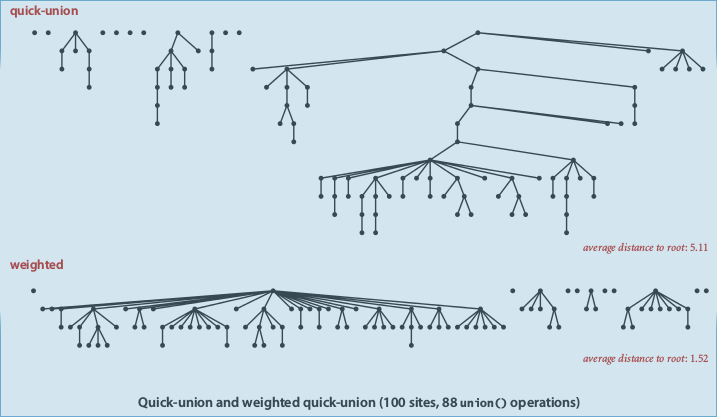
⇒ add an extra array: sz[] sz[i] is the size of the tree with root i

implementation

(数组int sz[] 初始全部为1)

• 依然需要root()函数.

  private int root(int p){ while(p!=id[p]) p=id[p]; return p; }

• FIND

  public boolean connected(int p, int q){ return root(p)==root(q); }

• UNION

  public void union(int p, int q){ int rp = root(p), rq=root(q); if(rp==rq) return; // if (sz[rp]<sz[rq]){ id[rp]=rq; sz[rq]+=sz[rp]; } else{...} }

complexity

FIND: proportional to depth of p and q in their tree UNION: const if p and q are root

• proposition

the max depth of weightedQuickUnion is lgN

[pf] considering a node x, in tree T1, dep(x) is x's depth in its tree.

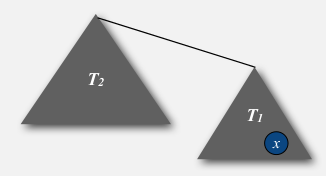
→ dep(x) will increase by 1, iff T1 is merged into another tree T2 (and by the algo, shoud have |T1|<=|T2| )
→ x's tree's size become |T1|+|T2| >= 2|T1| ⇒ everytime dep(x) increased by 1, x's tree's size will at least double*
at first dep(x)=1, if dep(x) increases lgN times, the size of the tree will be >= N
CQFD.

so the root() function takes only lgN time. conclusion: both UNION and FIND will be in lgN time.

improvement 2: path compression

• imporve the root() function:

when looking for root of a node ⇒ link all nodes in the path up to the root.
⇒ just a constant extra time compared to old implementation.

• 2 pass implementation:

  private int root(int p){ int r = p; while(r!=id[r]) r=id[r]; while(p!=r){ int t = p; p=id[p]; id[t]=r; } return r; }

flatens the tree greatly.

• single pass implementation:

just make all other node point to its grandparent (halving the path length) ⇒ not as flatening as before, but in practice will almost be the same. just one extra line of code: private int root(int p){ while(p!=id[p]){ id[p] = id[ id[p] ]; p=id[p];
} return p; }

complexity

(for weighet quick union with path compression — WQUPC)
very very small:

lg*() function: "iterated log function", lg(N) = the number of time to take log to get to 1 lg()几乎可以看成常数了:

ex. lg(65536) = 4* (x^16=65536)
because: lg(65536)=16 ; lg(16) = 4; lg(4)=2; lg(2)=1.
⇒ N obj, M unions will take (almost) linear time

(有人证明了不存在理论上linear的算法. )

conclusion: both UNION and FIND will be in constant time.

summery

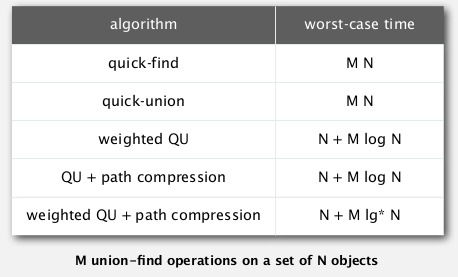
上面这个表格好像quick union的部分有问题? 最坏情况下应该是N+MN吧??
书上是这么写的:

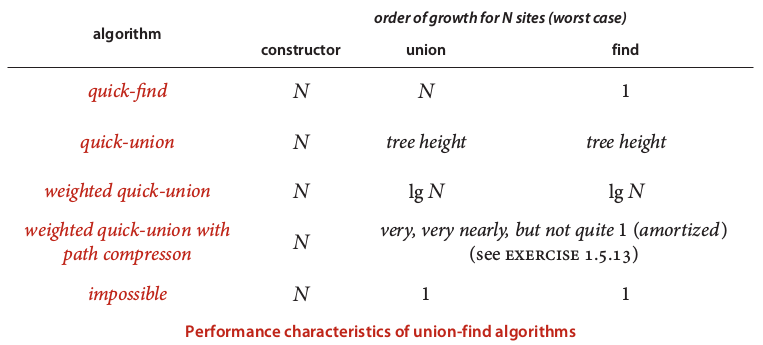
WQUCF reduce 30 years to 6 seconds.

5. Union Find Application

• percolation
• dynamic connectivity
• Kruskal MST algo
• Games (GO)
• .......

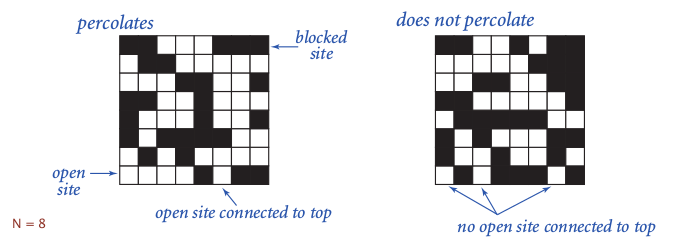
percolation

• model:

NN grid of sites
⇒ each site is open with proba=p*
⇒ sys percolate iff bottom and top are connected by open sites.

• question: the percolation probability as a function of p (phase transition)

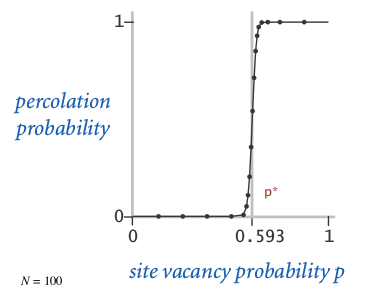
nobody knows how to get the threshold mathematically
⇒ run simulations to find out the phase transition threshold.

• Monte Carlo simulation

→ all sites initilized to be closed
→ randomly open sites one by one
→ when the sys percolates, the vacancy percentage is an estimate of p
*(run above simulation for millions of times)

implementation

• N^2 sites, named 0 to N^2-1

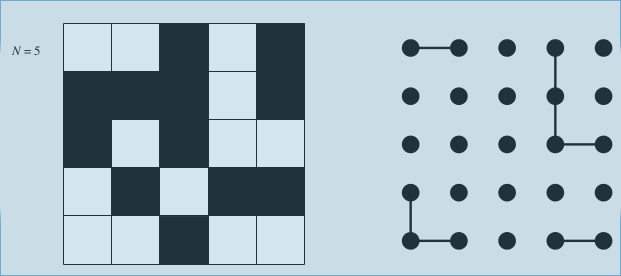
• add 2 more vertual sites: one on top, one on bottom

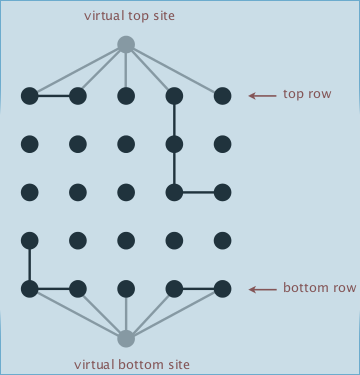
• openning a site: union to adjcent open sites (at most 4 unions)