Setting up your Maching Learning Application

Train / Dev / Test sets

Applied ML: highly iterative process. idea-code-exp loop

splitting data
splitting data in order to speed up the idea-code-exp loop:
*training set / dev(hold-out/cross-validataion) set / test set *

split ratio:

• with 100~10000 examples: 70/30 or 60/20/20
• with ~1M examples: dev/test set can have much smaller ratio, e.g. 98/1/1

mismatched train/test distribution
training and test set don't come from the same dist.

• rule of thumb: make sure dev and test set come from the same distribution.
• might be OK to only have dev set. — thought in this case no longer have unbiased estimate of performance.

Bias / Variance

• high variance: overfitting
• high bias: underfitting

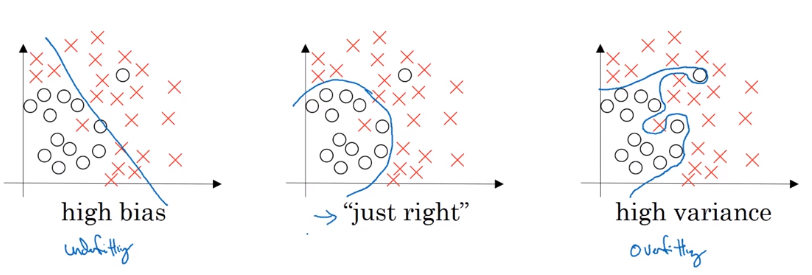
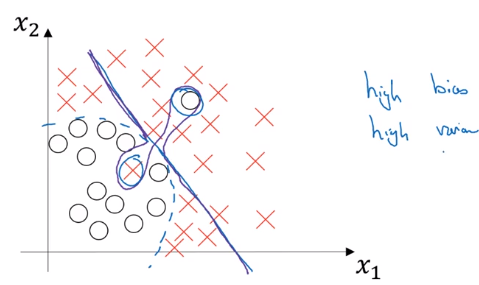
high base and high variance (worse case): high bias in some region and high variance elsewhere

how to estimate bias&variance
→ look at train and dev set error

• high variance: Err_train << Err_dev — not generalize well
• high bias: Err_train ~= Err_dev, and Err_train >> Err_human — not learning well even on training set
• high bias and high variance (worse): Err_train >> Err_human, Err_train >> Err_dev

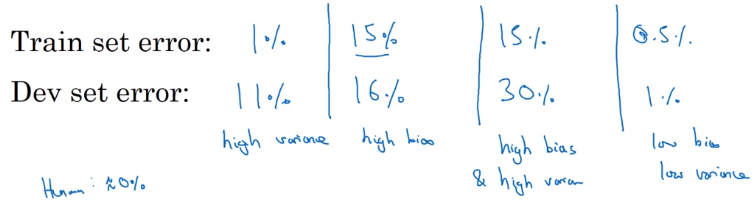
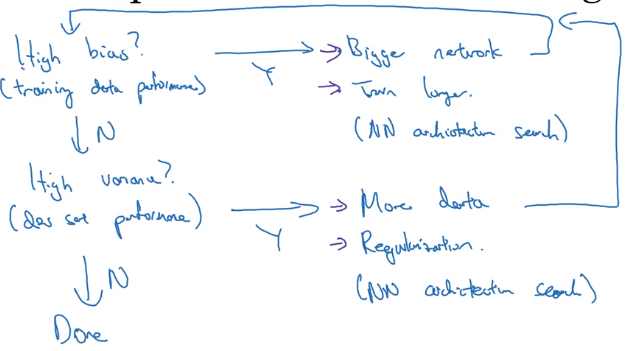
Basic Recipe for Machine Learning

basic recipe:

1. does algo have high bias ? (look at Err_train)
   • if yes → try bigger nn / other architecture
   • until having low bias (fit well training set)
2. high variance ? (look at Err_dev)
   • if yes → get more data / regularization / other architecture

bias-variance tradeoff

• in pre-DL era, bias and variance are tradeoff (decrease one → increase the other)
• in DL era: if getting bigger nn and more data always possible, both can be reduced

(when well regularized,) "training a bigger NN almost never hurts."

Regularizing your neural network

2 ways to reduce variance: regularize, or get more data.

Regularization

example: logistic regression

• params: w, b
• cost function J(w,b) = 1/m * L(yhat_i, yi)

→ add one more term to cost J: adding L2 norm of w(L2 regularization)
(lambda: regularization param)

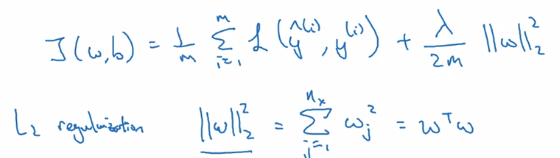
just omit regularizing b: w is high dim, b is single number.

L1 regularization: L1 norm of w → w will be sparse → compressing the model (just a little bit)
⇒ L2-reg is much often used

example: NN

• params: w[l], b[l] for l = 1..N
• sum of the norms of each w[l] matrix.

⇒ "Frobenius norm" of a matrix: sum (each element squared)

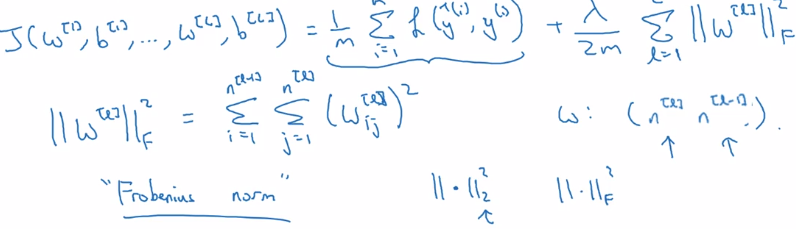
gradient descent: adding one more term from backprop
d(1/2m * ||w||) = lambda / m

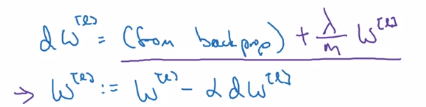
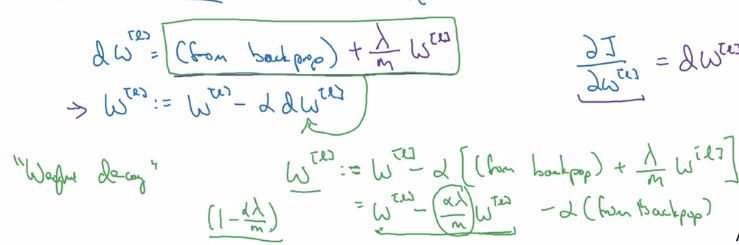
L2-reg also called "weight decay":
with L2-reg, looks as if doing the backprop updating, with w being w' = (1-alpha*lambda/m) * w (decayed w)

Why regularization reduces overfitting?

why imposing small params prevents overfitting?

intuition 1
→ heavy regularization
→ weight ~= 0
→ many hidden units' impact are "zeroed-out"
→ simpler NN

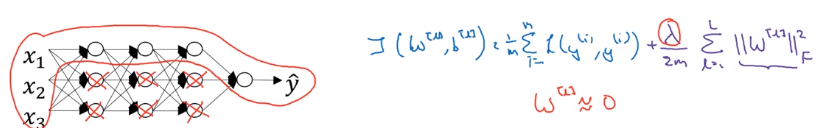
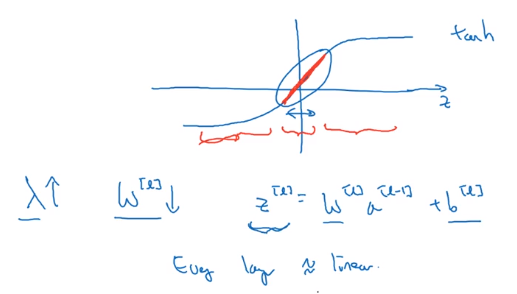
intuition 2
e.g. activation g(z) = tanh(z)
small z → g(z) ~= linear,
large z → g(z) flattend
⇒ large lambda → small w
→ z small
→ every layer ~linear

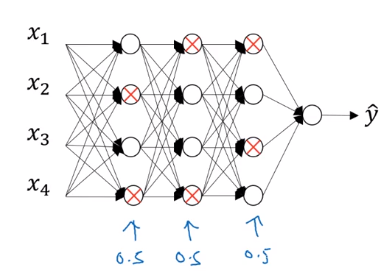
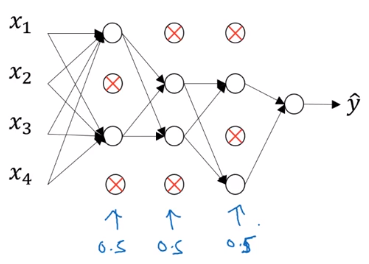
Dropout Regularization

another powerful method of regularization
dropout: For each training example, in each layer, eliminate randomly some of its output values.

dropout implementation: "inverted dropout"

example: dropout of layer 3, keep_prob = 0.8 (prob of keeping hidden unit)
→ generate a rand matrix of shape the same shape as activation a[3]

d3 = np.random.rand(a3.shape[0], a3.shape[1]) < keep_prob  # d3 is bool matrix  
a3 = np.multiply(a3, d3)  # element-wise multiply  
a3 /= keep_prob  # ****"inverted dropout"****

"inverted dropout": why a3 /= keep_prob (i.e. make a3 larger)?

• let's say layer 3 has 50 units, keep_prob = 0.8
• → ~10 units shut off
• z[4] = w[4] * a[3] + b[4]

⇒ a[3] have random 20% units shut off
→ w[4]a[3] will be reduced by 20% in expection*

• inverted dropout: a3 /= keep_prob, to keep expected value a3 remains unchanged.
• (No dropout at test time) → inverted dropout avoids scaling problem at test time

making predictions at test time
NOT use dropout at test time ⇒ don't want output to be random at test time...

Understanding Dropout

why randomly shut units prevents overfitting ?

Intuition: can't rely on any one input feature → have to spread out weight
spread weights ~→ smaller L2 norm (shrink weights)
Can be formally proven: dropout is equal to adaptive L2-reg, with penalty of different weight being different.

For one hidden unit: any of it input features (from prev layer) can go out at random

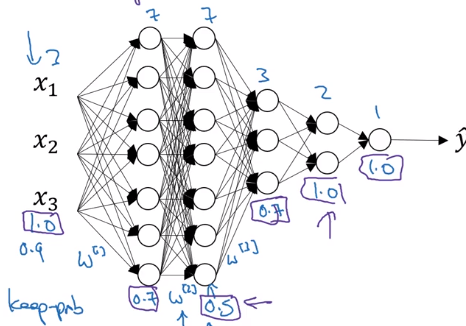
Implementation details

• vary keep_prob for different layer

→ smaller keep_prob for larger layer

• usually no dropout (or very small dropout) for input layer...

Downside of dropout
cost function J no longer well-defined (because output yhat is random)
→ can no longer plot cost-iter curve
→ turn off dropout before plotting the curve

Other regularization methods

data augmentation

adding more training example is expensive
→ vary existing training data (e.g. flipping/rand-distortions of training image for cats)

early stopping

plot Err or J to #iterations for both train and dev set.

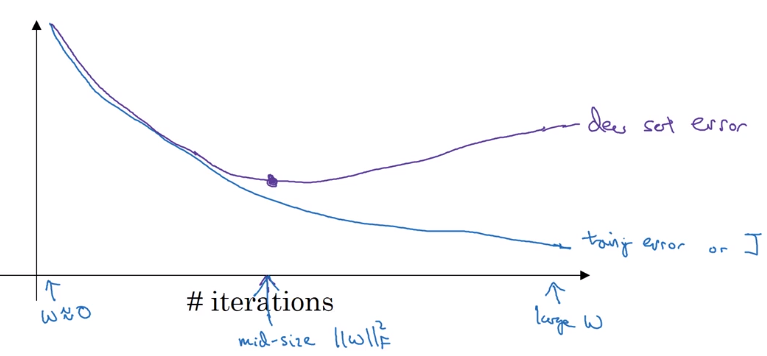
Downside of early-stopping:
optimization cost J and not overfitting should be separated task ("Orthogonalization")
→ early-stopping couples the two jobs.

upside of early stopping: no need to try different values of regularization param (lambda) → finds "mid-size w" at once.

Setting up your optimization problem

How to speed up training (i.e. optimize J)

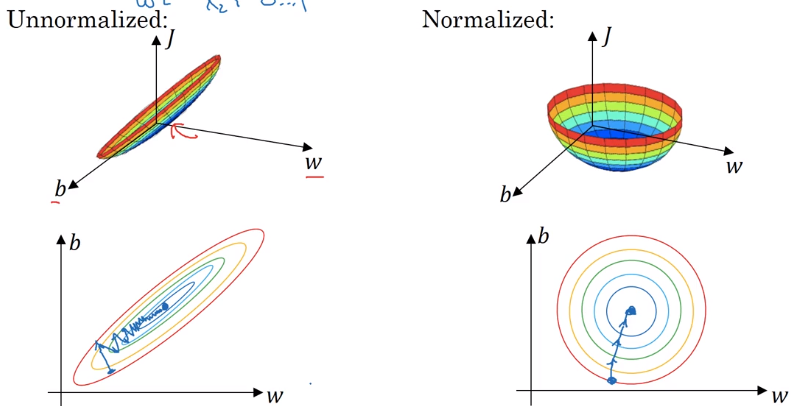
Normalizing inputs

normalize input:

1. substract mean
2. normalize variance

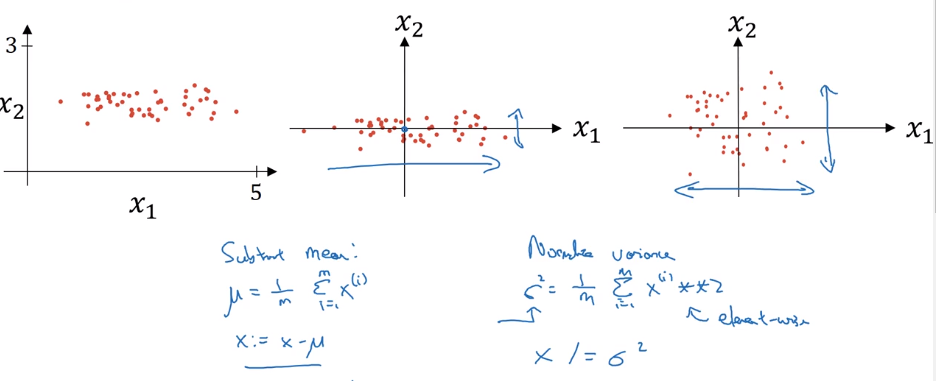
detail: in data splitting, use the same meu/sigma to normalize test set !

why normalizing input ?
if features x1 x2 are on different scales → w1 and w2 not same scale
J is more symmetric, easier to optimize

Vanishing / Exploding gradients

One problem in training very deep NN: vanishing/exploding gradients.

example: a very deep NN, each layer 2 units, linear activation g(z)=z, ignore bias b[l] = 0.

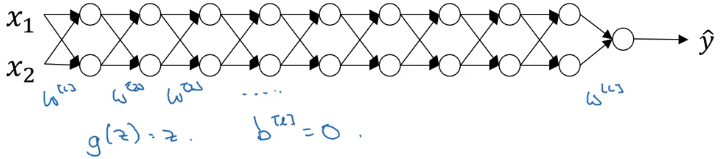
linear activations → y is just a linear transformation of x

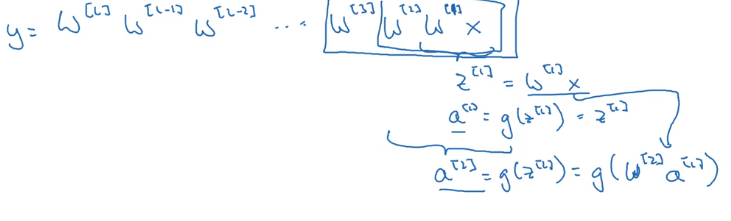
• assuming each w[l] = 1.5 * Identity_matrix ⇒ activations increase exponentially
• assuming each w[l] = 0.5 * Id ⇒ activations decrease exponentially

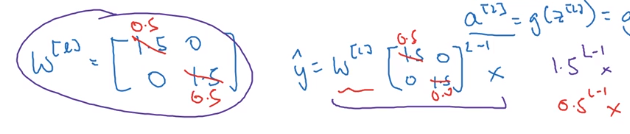
yhat too large or too small → hard to train

Weight Initialization for Deep Networks

A partial solution of vanishing/exploding gradient problem: carefully initialize weights.

single neuron example:

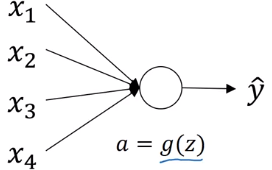
• y = g(w*x), g = relu
• n = # inputs for

z = w1x1 + ... + wnxn,
if wi are initzed randomly
→ large ns ⇒ z will be large !
⇒ set var(wi) = 1/n (2/n in practice) to keep z in similar scale for diffent #inputs
initialization code:
w[l] = np.random.randn(shape[l]) * np.sqrt( 2 / n[l-1] ) # n[l-1] = #inputs for layer-l

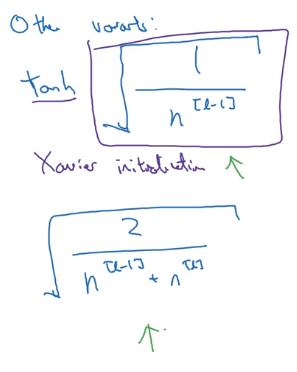
other variants
when activation function g = tanh
⇒ use var(wi) = 1/n ("Xavier initialization")

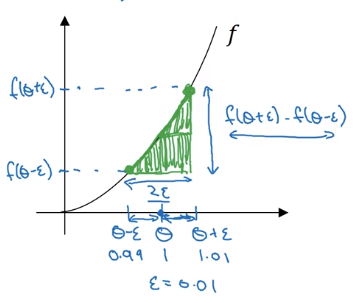
Numerical approximation of gradients

checking the derivative computation
example: f(x) = x ^ 3
→ vary x by epsilon to approximate f'(x), use 2-sided difference

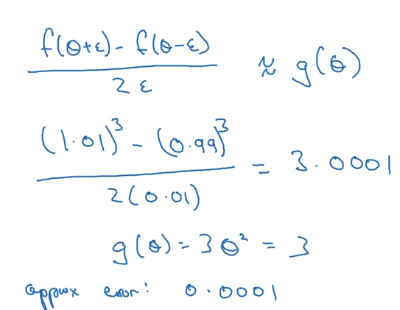
error order = O(epsilon^2) for 2-sided difference

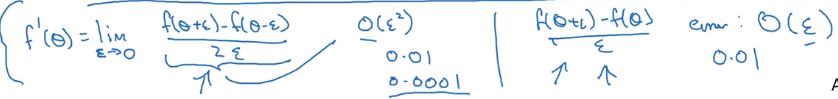
Gradient checking

Verify that your implementation is correct. — help finding out bugs in implementation early.

• concat all params into a big vector theta
• concat all dW[l] db[l] into big vector d_theta
• to check if d_theta is correct: construct a d_theta_approx vector

⇒

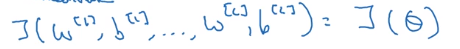
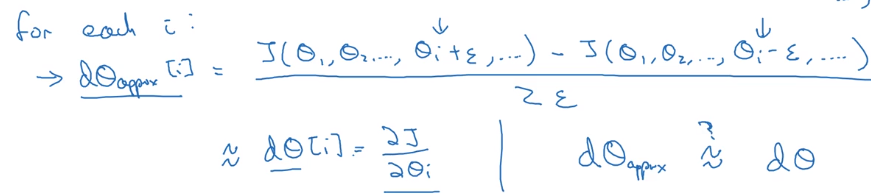
How to check "approximate":

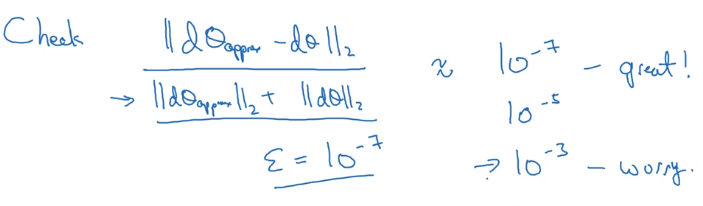
Gradient Checking Implementation Notes

• Dont' use checking in training: constructing d_theta_approx is slow
• When check fails: look at components to try to find bug
• Remember regularization: J contains reg term as well
• Doesn't work with dropout: J not well defined (random variable), turn dropout off before checking.
• Run check at random initialization (w,b~=0), then again after some training(w,b~>0)