1. Introduction
rearanging array of size N into ascending order
test client code: Insertion.sort(a);
sort any datatype
callback
callback = reference to executable code
i.e. passing functions as argument to sort() method
sort() function calls object's compareTo() method

→ implement the Comparable interface:
public class XX implements Comparable<XX>{
...
}
the interface:
public interface Comparable<Item>{
public int compareTo(Item that);
}
compareTo():
return -1 (if this<that)/+1/0;
needs a total order.
→ in the sort() implementation:
has not dependencies on type of data.
public static void sort(Comparable[] a){
if(a[i].compareTo(a[j])>0)...
}
helper functions
-
less
private static boolean less(Comparable v, Comparable u){ returnv.compareTo(u)<0; }
-
exch
private void exch(Comparable[] a, int i, int j) { Comparable swap = a[i]; a[i] = a[j]; a[j] = swap; }
-
isSorted
test if sorted if algo passes the test using only less ant swap, then it's correct.
2. Selection Sort
Idea: each time: find the minimum from the remaining items.
a[min] is the smallest element to right of a[i] ⇒ swap a[i] and a[min] (elements to left of i are sorted)
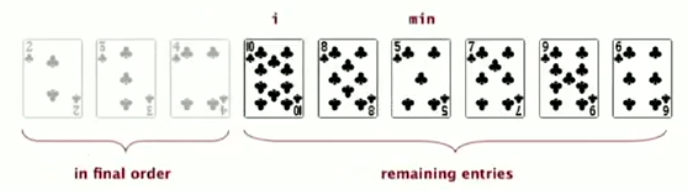
invariants
- entries to the left of i are in sorted order, and are fixed (in final position) ever since
- no entry to the right of i is smaller than any entry to the left of i
implementation
public class SelectionSort extends AbstractSorting{
//...
public static void sort(Comparable[] a){
for(int i = 0; i<a.length; i++){
int min = i;
for(int j = i+1; j<a.length; j++)
if(less(a[j],a[min]))
min = j;
exch(a,min,i);
}
}
}
analysis
proposition: selection sort uses N-1 + N-2 + ... + 1 = ~N^2/2 compares, and N exchanges. → quadratic time
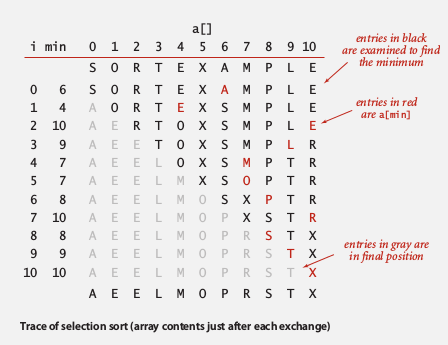
- insensitive to input: quadratic time even if input is already sorted.
- data movement is minimum: linear time of exchanges (every exchange puts an item to its final position)
3. Insertion sort
quite different performance characteritics than selection sort.
Idea: In iteration i: move all entries larger than a[i] to its left.
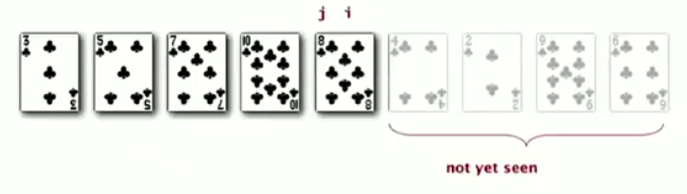
invariants
- entries to the left of i are in ascending order (but not in final position)
- entries to the right of i are not yet been seen
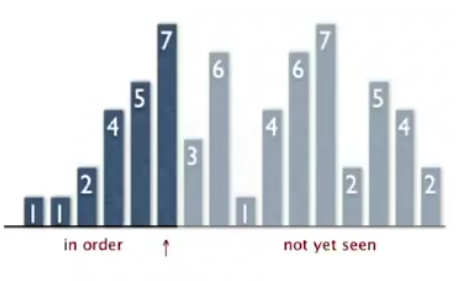
implementation
publc class InsertionSorting extends AbstractSorting{
public static void sort(Comparable[] a){
for(int i=1; i<a.length; i++)
for(int j=i; j>0; j--){
if(less(a[j],a[j-1]))
exch(a,j,j-1);
else break;
}
}
//...
}
analysis
proposition (average case):
(the performance on average — for randomly sorted array )

proof:
expect each entry to move halfway back

best case and worst case
best case if array already sorted min ascending order: N-1 compares, 0 exchanges.
worst case if array sorted in descending order: every element goes all the way back → 1/2N^2 compares, 1/2N^2 exchanges
partially sorted arrays
def." inversion" an inversion is a pair of entries that are out of order.
def. "partially sorted"
An array is called partially sorted if the number of inversions is <= cN. *
proposition.
Insertion sort runs in linear time for partially sorted array.
proof.
number of exchanges = number of inversions.
number of compares = number of exchanges + N-1
4. Shell Sort
First non-trival sorting methode: an improvement of insertion sort.
def. "h-sorted array"
an array is h-sorted if every h-interleaved subarray is sorted. (h=1: just a sorted array)

Idea: move entries >1 position at a time by h-sorting the array, then decrease h.
use decreasing sequences of value h:

implementation
How to h -sort
simply insertion sort with stride length=h.
why insertion sort:
for big h: small subarray
for small h: nearly in order
proposition
A g-sorted array remains g-sorted after h-sorting it.
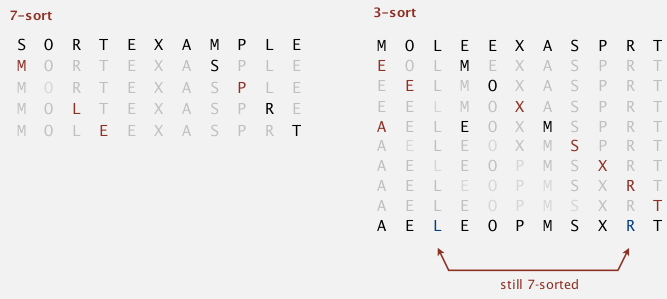
(subtle to prove...)
which sequence of h to use
3x+1 sequence proposed by Knuth. 1,4,13,40....
public class ShellSort extends AbstractSort{
public static void sort(Comparable[] a){
int h = 1, N=a.length;
while(h<N/3) h = h*3+1;//find the beginning h (N>h>N/3)
while(h>=1){//performs h-sort
for(int i= h;i<N;i+=h)
for(int j = i;j-h>=0;j-=h)
if( less(a[j],a[j-h]) )
exch(a,j,j-h)
else break;
h = h/3;
}
}
//...
private static boolean isHsorted(Comparable[] a, int h) {
for (int i = h; i < a.length; i++)
if (less(a[i], a[i-h])) return false;
return true;
}
}
每次hsort, 外围的循环是for(int i= h;i<N;i+=h), 需要理解一下: i移动一次以后, 进行的是另一个subarray 的插入排序, 当移动到N-1的时候所有subarray的插入排序才结束. (也就是说不是先完成一个subarray的插入排序再完成另一个, 这些是插入排序是同步进行的)
analysis
proposition (for worst case )

→ better than quadratic time !
property (found in practice)
of compares < Cte * N * (# of h used )
→ #compares < NlgN * Cte
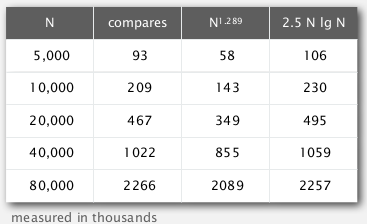
*accurate model has not been discovered *
(所以shellsort在实际使用中几乎和快速排序一样快! — 尽管没有数学证明来保证)
why we are interested in shell sort useful in practice:
- fast for medium sized arrays (beat even the classical sophistiated algorithms)
- tiny code volumn (used in embeded systems)
lead to interesting questions for 50 years:
- asymptotic growth rate ?
- best sequence of h ?
- average case performance ?
5. shuffling
shuffle array using sort
one way to shuffle an array:
- for each array entry, generate a random real number
- sort the array of real numbers
- ⇒ the original array is shuffled !
proposition
this shuffle sort produces a uniformly random permutation of input array
drawback: cost for sorting...
Goal: get uniformly random permutation in linear time.
Knuth shuffle
algo:
for i = [0,N):
- r = rand( [0~i] ) or rand( [i, N-1] )
- swap a[r] and a[i]
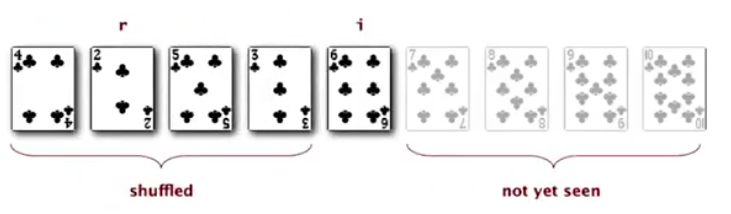
implementation:
public static void shuffle(Object[] a){
for(int i=0;i<a.length;i++){
int r = StdRandom.uniform(i+1);
exch(a,r,i);
}
}
proposition
Knuth algo produces an uniformly random permutation of input array.
proof.
Sufficient to prove that, for card i and position j, the proba(card i comes to position j) = 1/N.
- if i<=j, P = 1/j * j/(j+1) * (j+1)/(j+2) * ... * (N-1)/N
- if j<i, P = 1/i * i/(i+1) * (i+1)/(i+2) * ... * (N-1)/N
CQFD.
example: online poker
https://www.cigital.com/papers/download/developer_gambling.php ←那个扑克网站已经被黑出翔了...
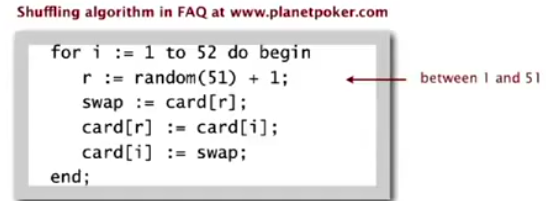
bugs:
- r never get 52 (52th card never moved)
- r = rand(N) instead of rand(0~i), → shuffle not uniform
- random() uses 32bit seed: only 2^32 possible shuffles, 2^32<52!
- seed = millisec from midnight, ~86*10^6 suffles
6. Convex Hull
application of sorting for the field of computational geometry.
convex hull
smallest polygoneenclosing all N points.
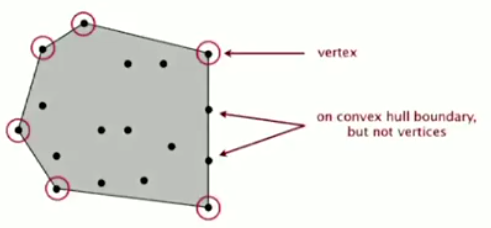
- input: N points
- output: sequence of vertices in counterclockwise (ccw) order.
application: robot motion planning; farest pair.
geometric properties:
- can traverse convex hull by making only ccw turns
- let p be the point with lowest y-coord, wrt p, vertices appear in increasing order of polar angle.
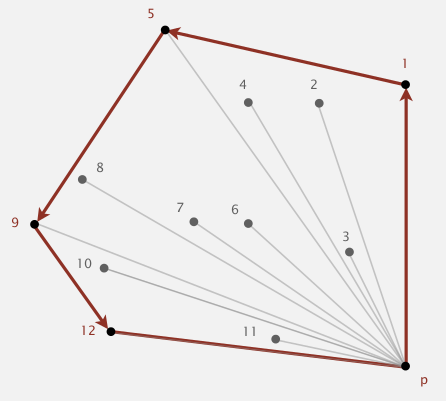
Algo
Graham scan algorithm:
* choose p with smallest y coord
* sort points by polar angle with p
* consider points in order (stack is used), discard unless creates a ccw turn.
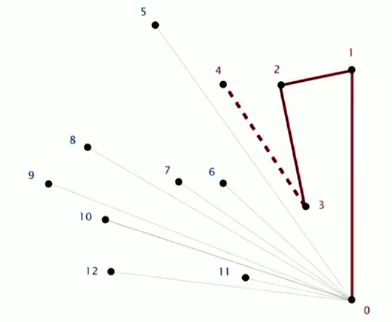
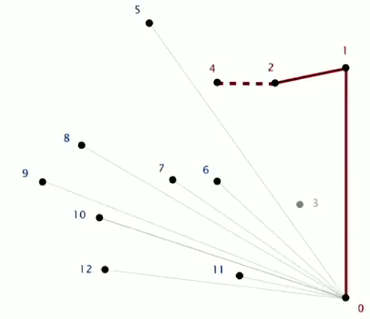
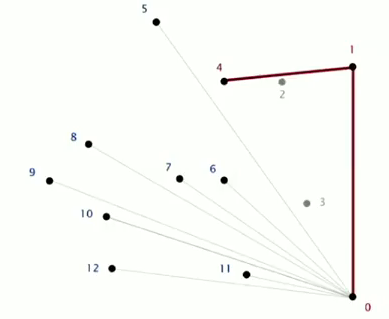
CCW
given three points a b c, returns if a→b→c is a CCW turn.
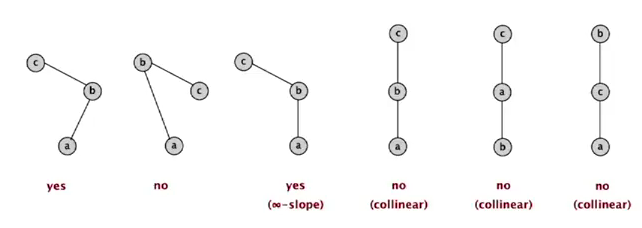
(assumption: no 3 points on a line)
⇒ calculate cross product of ab and bc ⇒ determinants!
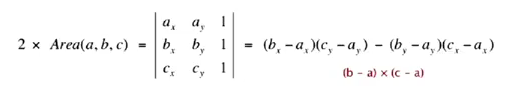
area>0 ⇔ CCW
implementation
public class Point2D{
private double x,y;
public static boolean ccw(Point2D a,Point2D b,Point2D c){
double area2 = (b.x-a.x)*(c.y-a.y) - (b.y-a.y)*(c.x-a.x);
return area2>0;
}
}
convex hull:
public static Stack<Point2D> GrahamScan(Point2D[] p){
//* assumes that points are sorted by polar angle in p[]
Stack<Point2D> hull = new Stack<Point2D>();
hull.push(p[0]);
hull.push(p[1]);
for(int i=2;i<p.length;i++){
Point2D b = hull.pop(), a = hull.peek(), c = p[i];
while(!Point2D.ccw(a,b,c)){
b = hull.pop();
a = hull.peek();
}
//now a,b,c makes a ccw turn:
hull.push(b);
hull.push(c);
}
}
running time: NlgN for sorting and linear for the rest.
Part 5 of series «Algorithms Princeton MOOC I»:
- [Algorithms I] Week 1-1 Union-Find
- [Algorithms I] Week 1-2 Analysis of Algorithms
- [Algorithms I] Week1-Lab: Percolation
- [Algorithms I] Week 2-1 Stacks and Queues
- [Algorithms I] Week 2-2 Elementary Sorts
- [Algorithms I] Week 3-1 Mergesort
- [Algorithms I] Week 3-2 Quicksort
- [Algorithms I] Week 4-1 Priority Queue
- [Algorithms I] Week 4-2a Elementry Symbol Tables
- [Algorithms I] Week 4-2b Binary Search Trees
- [Algorithms I] Week 5-1 Balanced Search Trees
- [Algorithms I] Week 5-2 Geometric Applications of BSTs
- [Algorithms I] Week 6 Hash Tables
Disqus 留言