week1

Created Friday 02 February 2018

Why sequence models

examples of seq data (either input or output):

• speech recognition
• music generation
• sentiment classification
• DNA seq analysis
• Machine translation
• video activity recognition
• name entity recognition (NER)

→ in this course: learn models applicable to these different settings.

Notation

motivating example: NER (Each word: whether the word is part of a person's name.)

• x^<t> / y^<t>: t-th element in input/output sequence.
• X^(i): i-th training example
• T_x^(i): length of i-th training example sequence

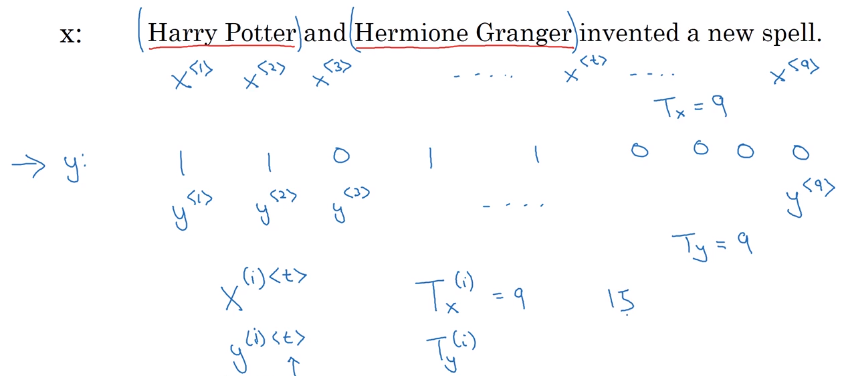
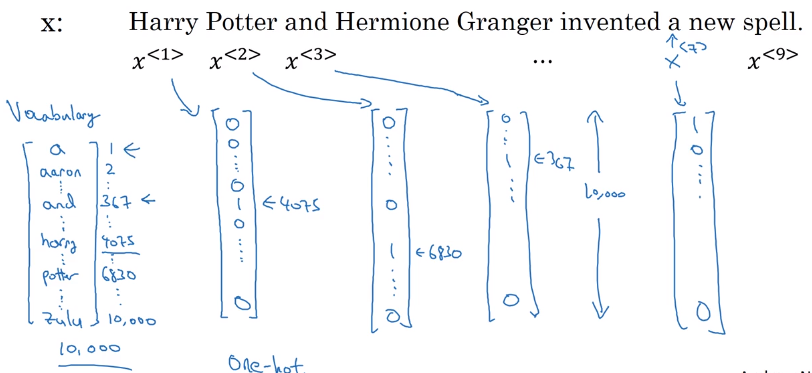
how to repr each words in a sentences (x)

• vocabulary: list of ~10k possible tokens (+"" for unknown words)
• one-hot repr for each word

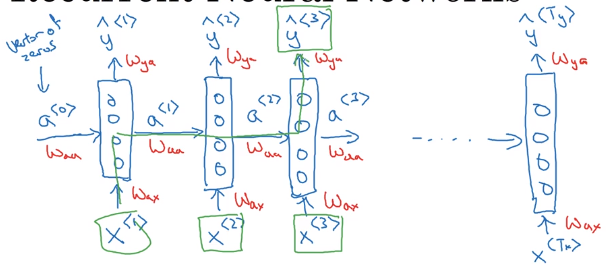
Recurrent Neural Network Model

why not a standard NN

• input/output are of different length (padding might not be a good representation)
• doesn't share features learned across different positions in text

→ using a better representation helps to reduce number of parameters.

RNN

motivation example: output length = input length

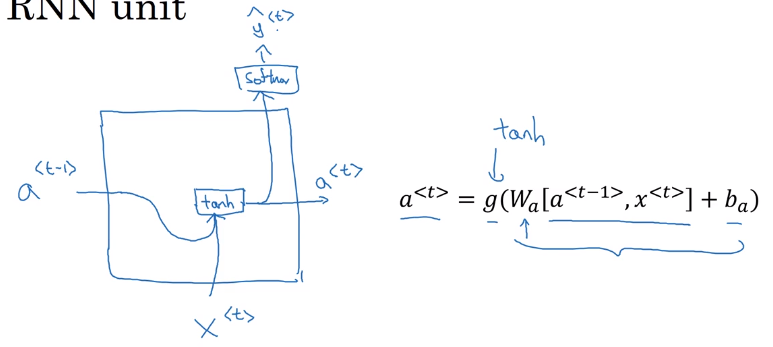
• for each input x<t>, → feed to RNN → compute activation(hidden state) a<t>, and output y<t>,
• y<t>=f(a<t>), a<t>=f(x<t>, a<t-1>), i.e. a depends on previous state and current input.
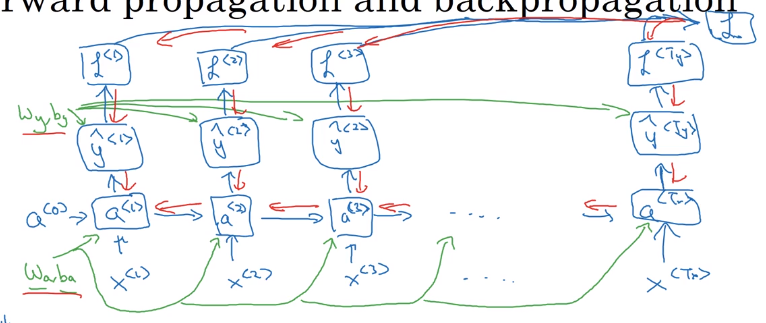
• parameters W_ax / W_aa / W_ya are shared across all time steps.

⇒ y<t> depends on x<1>...x<t>, limit: only depend on previous words ("unidirectional").

Unrolled diagram:

Or drawing a recurrent loop (harder to understand than unrolled version):

RNN Forward prop

formula to calculate a<t> and y<t>:
a = g(W_aa * a + W_ax * x + b_a)
y = g(W_ya * a + b_y)

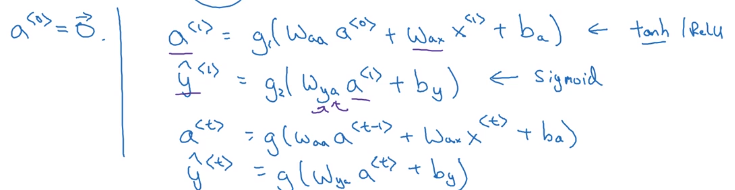
Simplified annotation: stack a<t-1> and x<t>, W_a = [W_aa, W_ax]

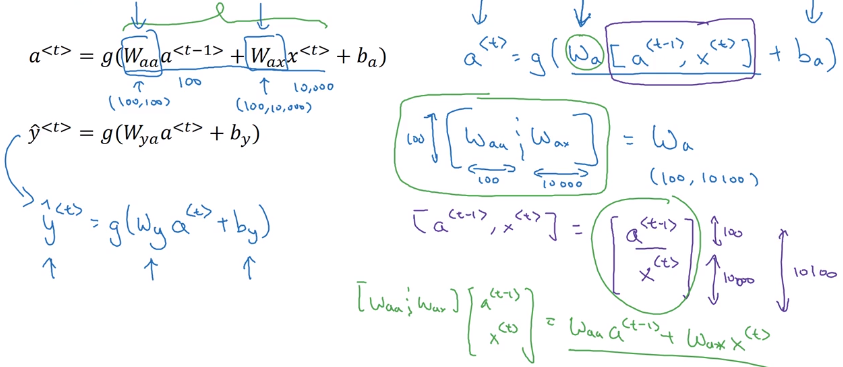
Backpropagation through time

Parameters: W_y and W_a
loss function: log loss at each timestep (assume predictions y are binary)

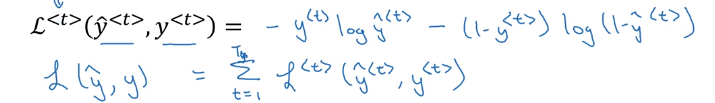
→ backporp through the computation graph:

Different types of RNNs

many-to-many:

• T_x = T_y, one prediction per timestep.

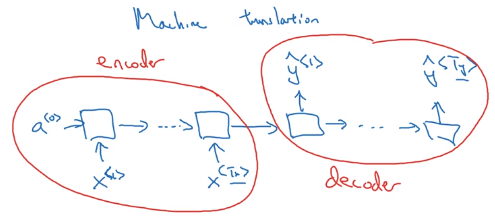
• T_x != T_y, e.g. machine translation

having a encoder and a decoder:

many-to-one:
e.g. sentence classification

one-to-many:
e.g. music generation

Language model and sequence generation

Language model
motivation example: speech recognition,
"The apple and the pear salad" VS "The apple and the pair salad"
language model: give probability of a sentence P(sentence).

Building language model with RNN
Training set: large corpus of text.

• tokenize
• vocabulary size
• unknow word "".

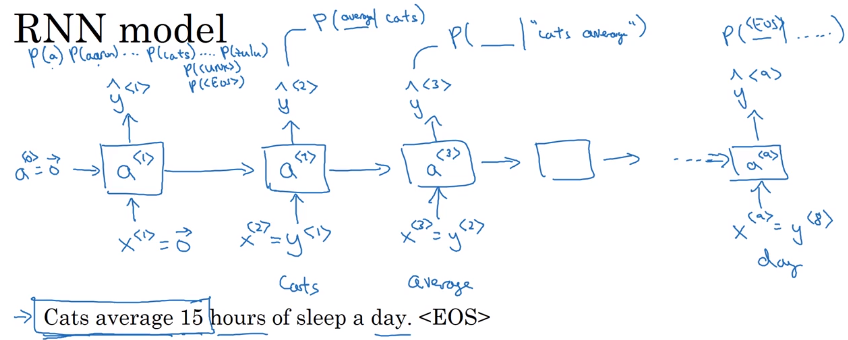
RNN for seq generation

• output y<t>: softmax of probability for each word.
• y<t+1>: make prediction given the correct previous word
• like this predict one word at a time.

Loss function: cross entropy (actual word VS probability of this word) at each timestep.

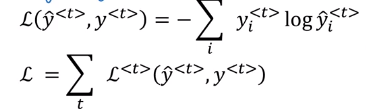
Sampling novel sequences

Get a sense of what's learned: sample nouvel seqs.
From training, the RNN has a distribution of sequences P(y<t> | y<1...t-1>).
In sample: let the model generate sequences (np.random.choice):

• feed previously gen word as input to next step
• include token in vocab to finish
• reject tokens

char-level language model

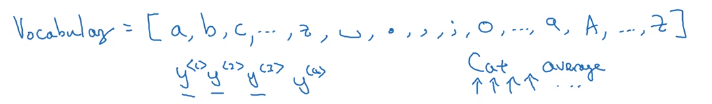
• pro: no token
• con: much longer sequences, more expensive to train.

Vanishing gradients with RNNs

long-range dependencies are hard to capture:
e.g. "the cat ........ was full" VS "the cats ...... were full"

this is due to vanishing gradients:

For exploding gradients: apply gradient clipping (restrict gradient norm).

Gated Recurrent Unit (GRU)

Modification of RNN to capture long range dependencies.

Visualization of a RNN unit:

(simplified) GRU

• Extra memory cell: c<t>=a<t>, (replaces output activation).
• Candidate value of c: c_tilde<t>=tanh(Wc * [c<t-1>, x<t>] + b_c)
• Gate (between 0 and 1, conceptually consider it as binary):

Gamme_u = sigmoid(W_u * [c<t-1>, x<t>] + b_u)
subscript "u" stands for "update", i.e. whether we want to update current memory cell

• Actual value of c<t> = Gamme_u * c_tilde<t> + (1-Gamma_u) * c<t-1> (* is element-wise multiplication)

i.e. c<t> can be conserved for long range before being updated

Visualization of GRU unit (maybe equations are more understandable...):

full GRU
for candidate c_tilde<t>, add one more gate Gamme_r: controlling how much c<t-1> contributes to c_tilde<t>("r" for "relevance", i.e. how relevant c<t-1> is for c_tilde<t>)

Long Short Term Memory (LSTM)

More powerful and general version of GRU.

• output a<t> no longer equals to memory cell c<t> (but a gated version of it, see below)
• candidate c_tilde<t> depends on a<t-1> instead of c<t-1>
• two update gates: Gamma_u (update gate) and Gamma_f (forget gate)
• output gate: Gamma_o
• value of c<t> = Gamma_u * c_tilde<t> + Gamma_f * c<t-1>
• value of a<t> = Gamma_o * c<t>

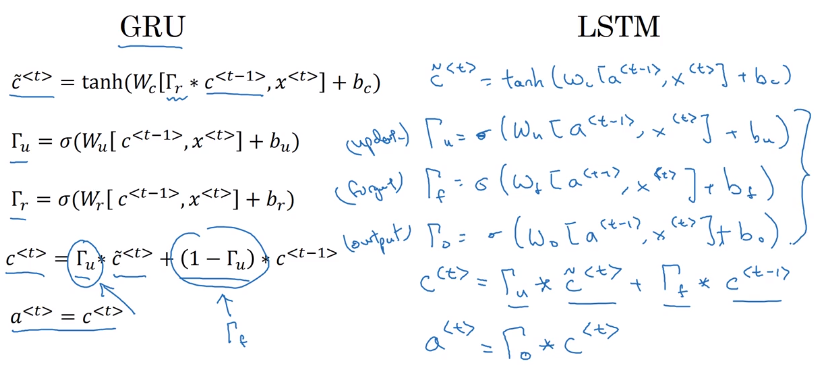
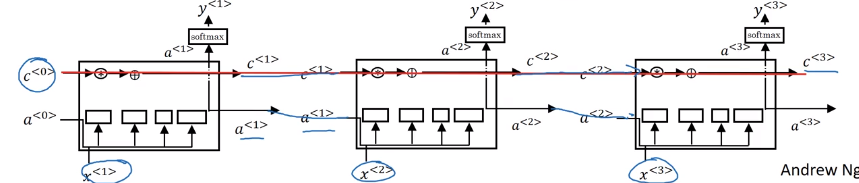
Visualization:

Intuition: c can be kept for long time if gates are set properly.

Variant: let the gates depend on c as well ("peephole connection")

GRU vs LSTM

• LSTM is proposed earlier
• GRU as a simplified version of LSTM
• GRU easier to train larger NN (2 gates instead of 3)
• LSTM more powerful, recommended default choice to try

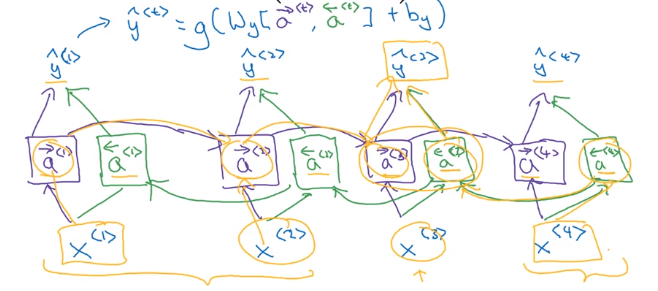
Bidirectional RNN

Getting information from the future.
motivation example:

Bidirectional RNN (BRNN)

• forward and backword recurrent components
• computation graph is still acyclic
• at t, both information from the past and the future are passed in
• BRNN with LSTM blocks are typically the first thing to try in NLP problems

Deep RNNs

Complex NN: stack multiple RNNs (having 3 RNN layers is already a lot).0
notation: a[l]<t> for activation in layer l and time t.