[Scala MOOC I] Lec2: Higher Order Functions

This week, we'll learn about functions as first-class values, and higher order functions. We'll also learn about Scala's syntax and how it's formally defined. Finally, we'll learn about methods, classes, and data abstraction through the design of a data structure for rational numbers.

2.1 - Higher-Order Functions

higher order functions: functions that takes functions as parameter or returns functions.

example:
⇒ put the f as a parameter

def sum(f:Int => Int, a: Int, b: Int):Int = { 
  if(a>b) 0 
  else f(a) + sum(f, a+1, b) 
}

function types

A => B is a function that takes A as parameter and returns B.

Anonymous functions

"literals" for functions, syntactic sugar. ex.

(x: Int, y: Int) => x+y (x: Int) => x*x

use anon functions in previous sum() function:

sum(x=>x, 1, 10) 
sum(x=>x*x, 1, 10)

exercice: turn sum() into tailrec fashion.

def sum2(f:Int => Int, a: Int, b: Int):Int = { 
  @tailrec 
  def sumTR(a: Int, acc: Int): Int = { 
    if (a > b) acc 
    else sumTR(a + 1, acc + f(a)) 
  } 
  sumTR(a, 0) 
}

(note: using namescoping to eliminate parameters in inner functions)

2.2 - Currying

define a function that returns a funtion

def sum3(f:Int => Int): (Int, Int)=>Int = { 
  def sumF(a:Int, b:Int):Int = { 
    if(a>b) 0 
    else f(a) + sum3(f, a+1, b) 
  } 
  sumF 
}

when calling this function:
sum3(cube)(1,10)

syntactic sugar: shorter version of functions that return functions:

def sum3(f:Int => Int)(a:Int, b:Int):Int = { 
    if(a>b) 0 
    else f(a) + sum3(f)(a+1, b) 
}

question: what is type of sum3? → Int => Int => (Int, Int) => Int note: functional types are associated to the right,
Int => Int => Int is equivalent to Int => (Int => Int)

"currying"

exercice:

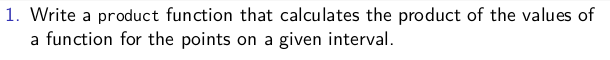
def product(f: Int => Int)(a: Int, b: Int): Int = { 
  if (a > b) 1 
  else a * product(f)(a + 1, b) 
} 
product(x=>x)(1,10)

def fact(n:Int) = product(x=>x)(1,n) 
fact(10)

def more_general(op: (Int,Int) => Int, default: Int) (f: Int=> Int)(a:Int, b:Int):Int = { if(a>b) default else op(a, more_general(op, default)(f)(a + 1, b)) } more_general((x,y)=>x+y, 0)(x=>x)(1,10)

老师的解法:
def map_reduce(f:Int=> Int, op:(Int, Int)=>Int, default:Int) (a:Int, b:Int):Int = { if(a>b) default else op(f(a), map_reduce(f, op, default)(a+1,b)) } def factorial2(n:Int):Int = map_reduce(x=>x, (a,b)=> a*b, 1)(1,n) factorial2(10)

2.3 - Example: Finding Fixed Points

find the fix point of a function: x = f(x)

val tol = 0.001 
def isCloseEnough(x:Double, y:Double):Boolean = 
  math.abs((x-y)/x)<tol 
def fixedPoint(f: Double=>Double)(firstGuess:Double):Double = { 
  def iterate(guess:Double):Double = { 
    if(isCloseEnough(guess, f(guess))) guess 
    else iterate(f(guess)) 
  } 
  iterate(firstGuess) 
} 
fixedPoint(x=>1+x/2)(1)

using the fixepoint function for sqrt:

• sqrt(x) = y such that: x=y*y
• =y such that y = x/y

• =fixed point for the function f(y)=x/y

  def sqrt(x:Double):Double = fixedPoint(y=>x/y)(1) sqrt(2)

⇒ doesn't converge! ⇒ guess oscillates between 1 and 2... average damping: prevent the estimate from varying to much. ⇒ by taking the average of successive values

def sqrt2(x: Double): Double = fixedPoint(y => (y + x / y) / 2)(1)

abstract this damping technique:

def avgDamping(f:Double=> Double)(x:Double):Double = 
  (f(x)+x)/2 
def sqrt2(x: Double): Double = fixedPoint(avgDamping(y=>x/y))(1)

summary: The highest level of abstraction is not always the best, but it is important to know the techniques of abstraction, so as to use them when appropriate.

2.4 - Scala Syntax Summary

notations(EBNF):

• | denotes an alternative
• [...] an option (0 or 1)
• {...} a repetition (0 or more)

Types

Expressions

Definitions

2.5 - Functions and Data

example. rational numbers (x/y) define a class:

class Rational(x:Int, y:Int){ 
  def numer = x 
  def denom = y 
} 
val x = new Rational(1,2) 
x.numer 
x.denom

this definition creates both a class and the constructor.
now implement arithmetic:

def add(that: Rational) = 
  new Rational(numer * that.denom + denom * that.numer, that.denom * denom)

def neg = new Rational(-numer, denom)

def sub(that: Rational) = 
  add(that.neg)

override def toString = numer + "/" + denom

2.6 - More Fun With Rationals

simplify the rationals at construction: add private members:

private def gcd(a: Int, b: Int): Int = if (b == 0) a else gcd(b, a % b) 
private val g = gcd(x, y) 
def numer = x/g 
def denom = y/g

other options:

• replace g with gcd(x,y)
• turn numer and denom into val

add less and max function:

def less(that:Rational) = 
  this.numer*that.denom < this.denom*that.numer

def max(that:Rational) = if(this.less(that)) that else this

preconditions

ex: avoid divide by 0.

require(y!=0, "denominator must be non zero")

→ java.lang.IllegalArgumentException: requirement failed: denominator must be non zero

requireis a test to perform when the class is initialized.
similar: assert()

constructor

in scala a class implicitly introduces a primary constructor:

• takes parameters of the class
• executes all statements in the class body

to add another constructor:

def this(x:Int) = this(x,1)

exercice:

override def toString = { 
  val g = gcd(numer, denom) 
  numer/g + "/" + denom/g 
}

2.7 - Evaluation and Operators

evaluation for class/object

extend the substitution model to classes and objects

examples:

operator overloading

infix ops

any method with one parameter can be used as an infix operator.

scala identifiers can bu symbolic:

⇒ change names to +, <, -, use in this way:

x + y 
x < y 
x max y 
x - y - z

unitary ops

now change the neg method: prefix operator, and might be confused with the sub(-) ⇒ it's name is special: unary_-

def unary_- = new Rational(-numer, denom)

precedence of ops

the precedence of an op is defined by its first letter order (by increasing precedence):

quite the same as in java

Programming Assignment: Functional Sets

Mathematically, we call the function which takes an integer as argument and which returns a boolean indicating whether the given integer belongs to a set, the characteristic function of the set. For example, we can characterize the set of negative integers by the characteristic function (x: Int) => x < 0.

Therefore, we choose to represent a set by its characterisitc function and define a type alias for this representation:

type Set = Int => Boolean 
def contains(s: Set, elem: Int): Boolean = s(elem)