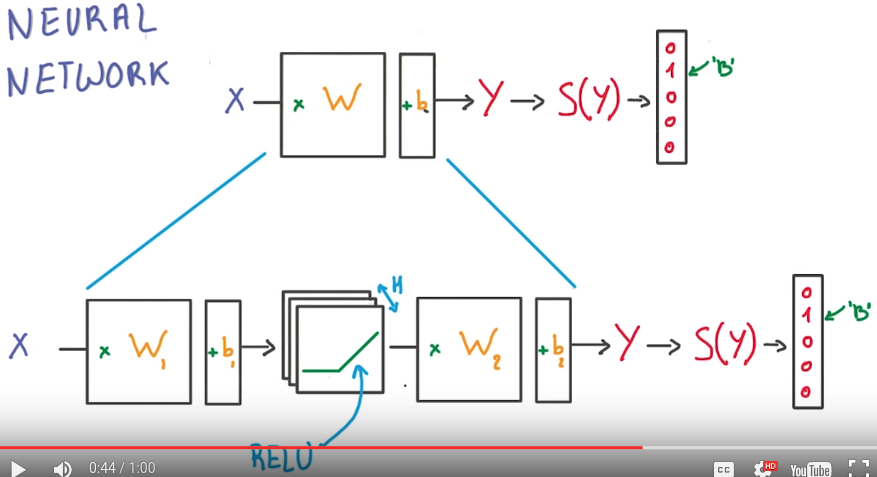
Linear models
matrix multiplication: fast with GPU
numerically stable
cannot cocatenate linear units → equivalent to one big matrix...
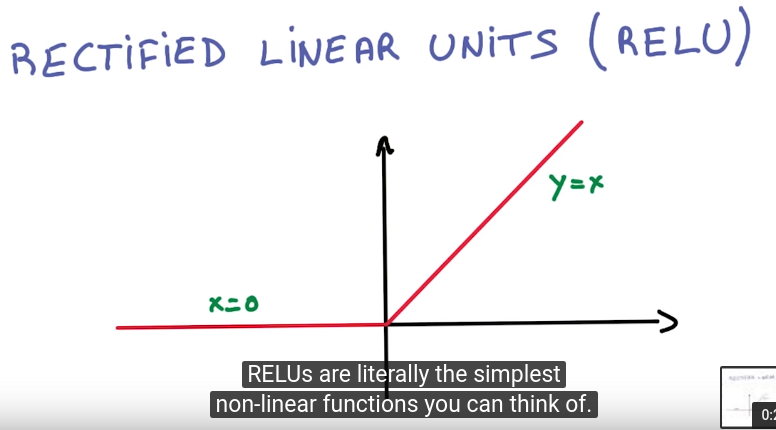
⇒ add non-linear units in between
rectified linear units (RELU)
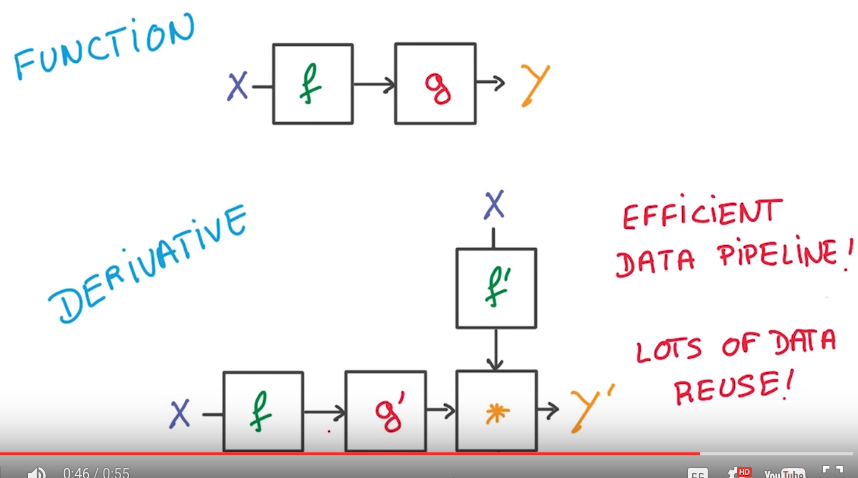
chain rule: efficient computationally
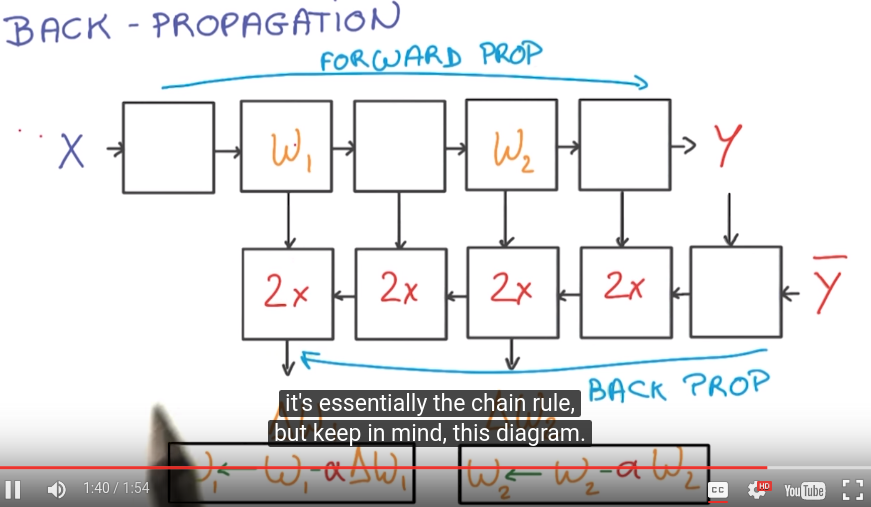
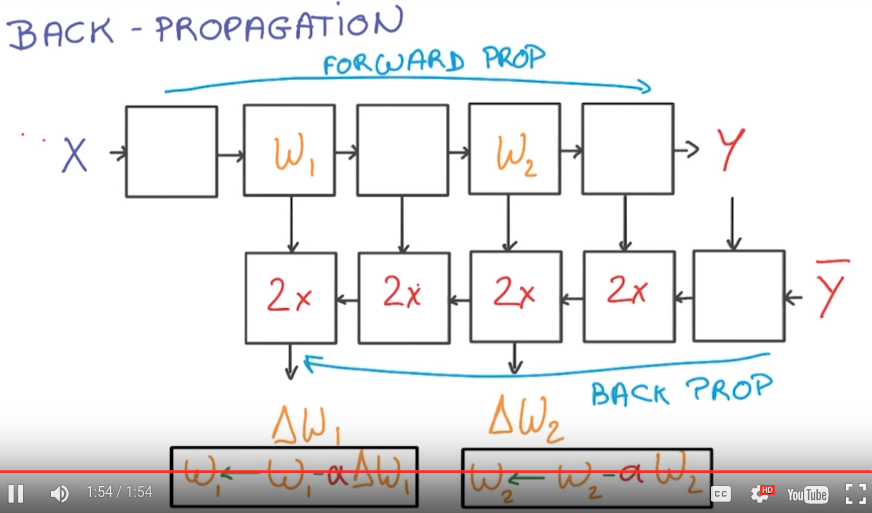
back propagation
easy to compute the gradient as long as the function Y(X) is made of simple blocks with simple deritivates.
most deep-learning framework can do it automatically for you.
N.B. The backprop block takes 2x memory/compute wrt the forward prop blocks.
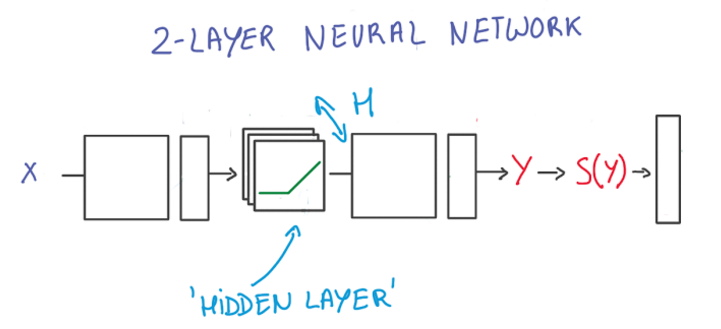
first neural network: RELU units between linear classifiers:
Tensor flow
tensors define computations, and they are nodes in a computation graph.
To actually run the optimization, use sessions...
define a computation graph:
batch_size = 128
num_hidden = 1024
graph = tf.Graph()
with graph.as_default():
# Input data. For the training data, we use a placeholder that will be fed
# at run time with a training minibatch.
tf_train_dataset = tf.placeholder(tf.float32,
shape=(batch_size, image_size * image_size))
tf_train_labels = tf.placeholder(tf.float32, shape=(batch_size, num_labels))
tf_valid_dataset = tf.constant(valid_dataset)
tf_test_dataset = tf.constant(test_dataset)
# Variables for linear layer 1
W1 = tf.Variable(
tf.truncated_normal([image_size * image_size, num_hidden]))
b1 = tf.Variable(tf.zeros([num_hidden]))
# Hidden RELU input computation
y1 = tf.matmul(tf_train_dataset, W1) + b1
# Hidden RELU output computation
X1 = tf.nn.relu(y1)
# Variables for linear layer 2
W2 = tf.Variable(
tf.truncated_normal([num_hidden, num_labels]))#W2
b2 = tf.Variable(tf.zeros([num_labels])) #b2
# logit (y2) output
logits = tf.matmul(X1, W2) + b2
loss = tf.reduce_mean(
tf.nn.softmax_cross_entropy_with_logits(logits, tf_train_labels))
def getlogits(X):
y1 = tf.matmul(X, W1) + b1
X1 = tf.nn.relu(y1)
return tf.matmul(X1, W2) + b2
# Optimizer.
optimizer = tf.train.GradientDescentOptimizer(0.5).minimize(loss)
# Predictions for the training, validation, and test data.
train_prediction = tf.nn.softmax(logits)
valid_prediction = tf.nn.softmax( getlogits(tf_valid_dataset) )
test_prediction = tf.nn.softmax( getlogits(tf_test_dataset))
run sgd optimization:
num_steps = 3001
with tf.Session(graph=graph) as session:
tf.initialize_all_variables().run()
print("Initialized")
for step in range(num_steps):
# Pick an offset within the training data, which has been randomized.
# Note: we could use better randomization across epochs.
offset = (step * batch_size) % (train_labels.shape[0] - batch_size)
# Generate a minibatch.
batch_data = train_dataset[offset:(offset + batch_size), :]
batch_labels = train_labels[offset:(offset + batch_size), :]
# Prepare a dictionary telling the session where to feed the minibatch.
# The key of the dictionary is the placeholder node of the graph to be fed,
# and the value is the numpy array to feed to it.
feed_dict = {tf_train_dataset : batch_data, tf_train_labels : batch_labels}
_, l, predictions = session.run(
[optimizer, loss, train_prediction], feed_dict=feed_dict)
if (step % 500 == 0):
print("Minibatch loss at step %d: %f" % (step, l))
print("Minibatch accuracy: %.1f%%" % accuracy(predictions, batch_labels))
print("Validation accuracy: %.1f%%" % accuracy(
valid_prediction.eval(), valid_labels))
print("Test accuracy: %.1f%%" % accuracy(test_prediction.eval(), test_labels))
Regularization
- early termination: stop when cannot improve in validation performance.
- L2 regularization: adding L2 norm of
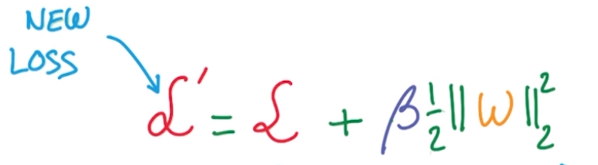
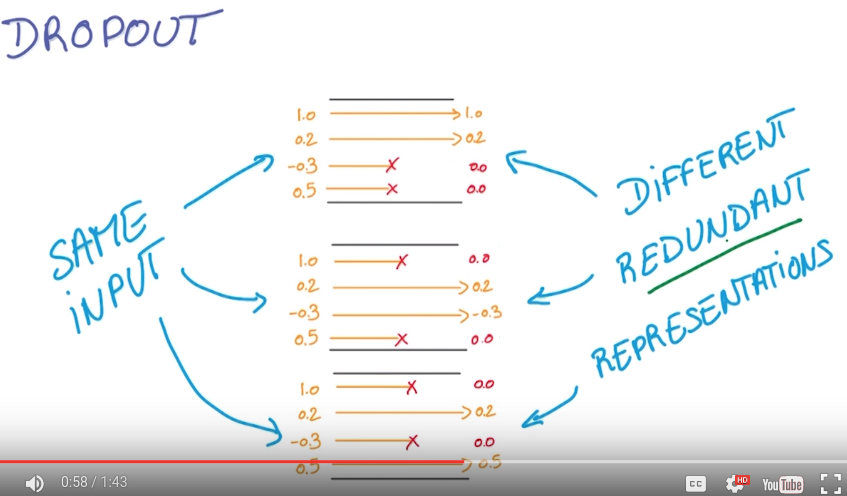
Dropout
def. activation is the output of last layer that flows into the next layer.
dropout: randomly set half of activations to 0.
rational: forcing your model to learn reduadant representations (consus over an ensemble of nns...)...
N.B.
for evaluation no longer dropout, ye = average of activations, trick to let ye=E(yt), in training, multiply the remaining activations by 2.

Disqus 留言