1. Introduction
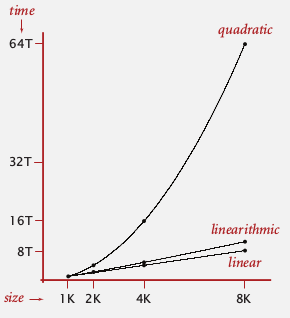
2. Observations
ex. 3-SUM pb
given N distinct numbers, how many triples sum up to 0? (pb related to computatioal geogtry)
- brute force method:
for(int i=0;i<N;i++)
for(int j=i+1;j<N;j++)
for(int k=j+1;k<N;k++)
{if(a[i]+a[j]+a[k]==0)
count++;
}
- mesuring running time:
stdlib.jar里面提供了一个Stopwatch类用于记录运行时间.

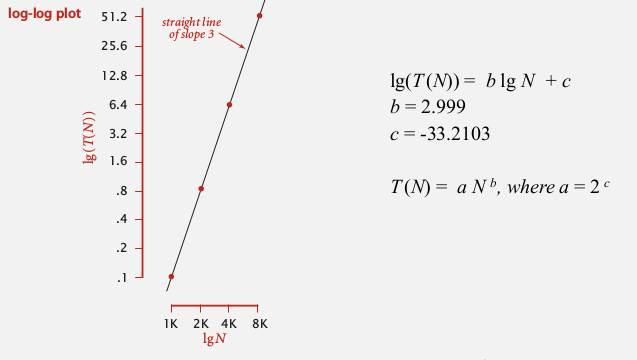
- log-log plot
T(N) = running time for input of size N
log(N)-log(T(N)) plot:
often get a straight line — power law
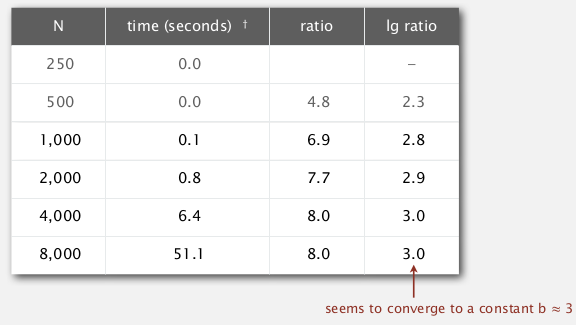
- doubling ratio:
(for checking the power law relationship, checking the power order)
each time double the size of input, then take log of the time ratio of 2 runs: log( T(2N)/T(N) )
3.Mathematical Models
- total running time: sum of cost*frequency of operations
-
cost of some basic operations:
- array allocation: c*N (because all array entries have to be set to 0/false/null)
- string concatenation: c*N (proportional to the length of string !)
-
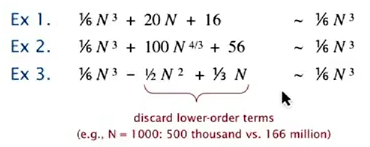
simplification
crude analysis
ignore lower terms tilde notation

- estimating discrete sum by relaxation
Replace the sum with an integral, and use calculus — 很机智...
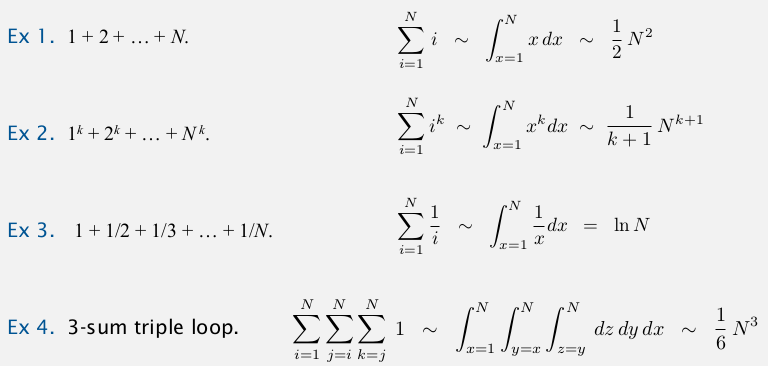
4. Order of Growth Classification
(discard the leading coefficient when considering the growth order)
- only a small set of growth functions:
1, logN, N, NlogN, N^2, N^3, 2^N
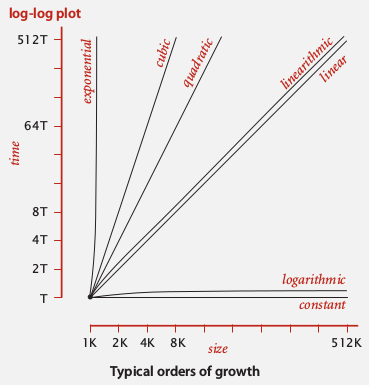
- exemples:
binary search ⇒ logN
divide and conquer ⇒ NlogN
exhaustive search ⇒ 2^N
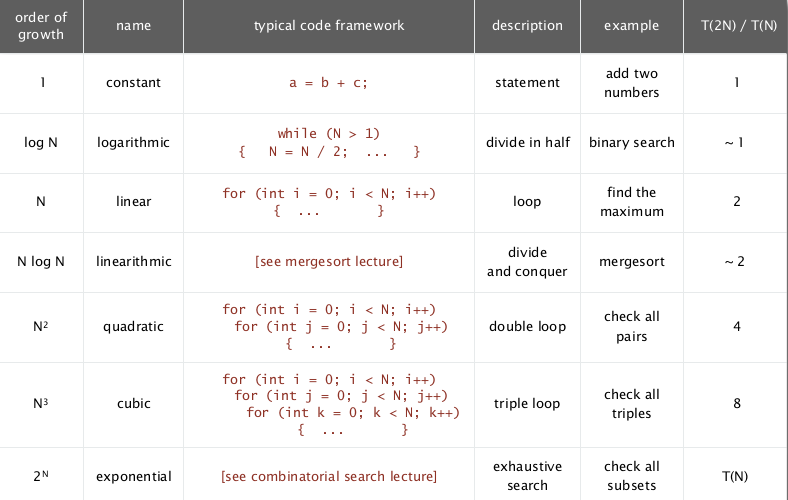
practical performance:
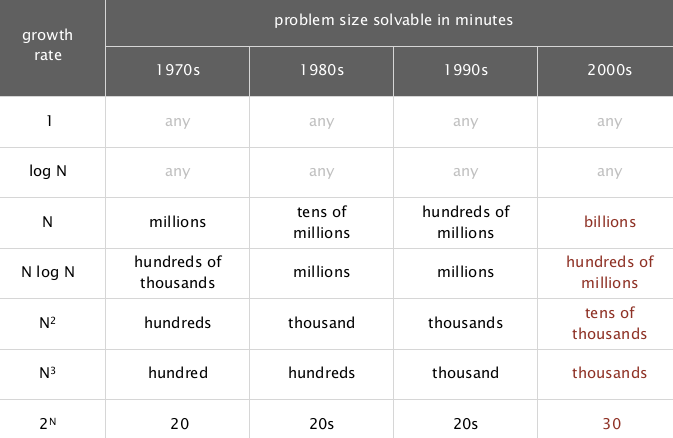
-
ex. binary search
public int binearch(int arr[], int key){//arr[] already sorted int lo=0,hi=arr.length; while(i<j){ int m = (lo+hi)/2; if(arr[m]==key) return m; else if(arr[m]<key) lo=m+1; else hi=m-1; } return -1; }
(→ Bug in Java's Arrays.binarySearch() discovered in 2006......)
→ invariant: if key in arr, arr[lo]<=key<=arr[hi]
proposition. binary search uses at most logN+1 compares to search a sorted array of size N.
pf.
denote T(N) := nb of compares for array with size <=N
→ T(1)=1
→ recurrence relation: T(N)<=T(N/2)+1
⇒ T(N)=logN
- a faster 3-SUM
→ first sort the array (~NlogN)
→ for any pair a[i] and a[j], do binary search for -(a[i]+a[j]) ~(N2LogN)
⇒ reduce from N3 to N2logN ! (for 8k numbers, running time goes from 51s to 0.96s)
5. Theory of Algorithms
-
types of analysis
-best case -worst case -average case(random input, "expected cost")
-
notations
big Theta/big O/big Omega
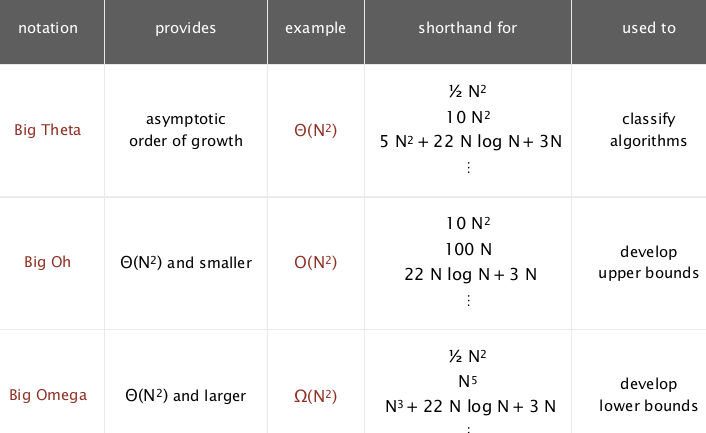
- big O: upper bound → * once a specific algo is found, find an upper bound
- big Omega: lower bound → proove that no algo can do better
- big Theta: symptotic growth (same order, optimal algo) → lower and upper bound match*
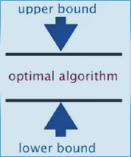
⇒ in this course: use tilde notation: contain leading constants for highest order term
6. Memory
KB: 2^10 bytes
MB: 2^20 bytes (1 million)
GB: 2^30 bytes (1 billion)
64-bit machines: 8 byte pointers
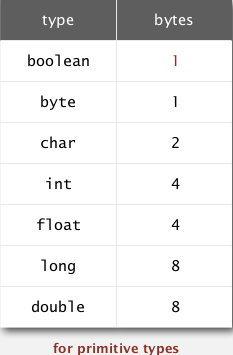
- typical memory usage:
for primary types:
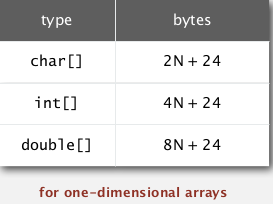
for arrays (with array overhead=24bytes) :
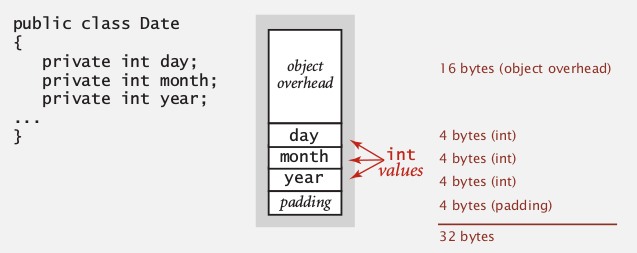
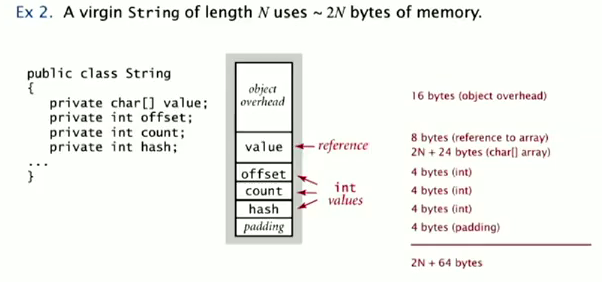
Obj overhead: 16 bytes (obj的大小=16+obj内部filed的大小)
references: 8 bytes (ex. inner class has a ref to encolsing class)
padding: each obj uses a multiply of 8 bytes (obj大小=8 bytes的整数倍)
Part 2 of series «Algorithms Princeton MOOC I»:
- [Algorithms I] Week 1-1 Union-Find
- [Algorithms I] Week 1-2 Analysis of Algorithms
- [Algorithms I] Week1-Lab: Percolation
- [Algorithms I] Week 2-1 Stacks and Queues
- [Algorithms I] Week 2-2 Elementary Sorts
- [Algorithms I] Week 3-1 Mergesort
- [Algorithms I] Week 3-2 Quicksort
- [Algorithms I] Week 4-1 Priority Queue
- [Algorithms I] Week 4-2a Elementry Symbol Tables
- [Algorithms I] Week 4-2b Binary Search Trees
- [Algorithms I] Week 5-1 Balanced Search Trees
- [Algorithms I] Week 5-2 Geometric Applications of BSTs
- [Algorithms I] Week 6 Hash Tables
Disqus 留言