1. Introduction to Maxflow

Min-cut pb

• input: edge-weighted digraph G, each edge e has weight("capacity") c[e]>=0, a source vertex s, a target vertex t.
• def. an st-cut (A,B) is a partition of vertices into 2 disjoint sets A and B, with s in set A and t in set B.
• def. the capacity of a cut (A,B) is sum of capacities of edges going from A to B (not considering B to A).

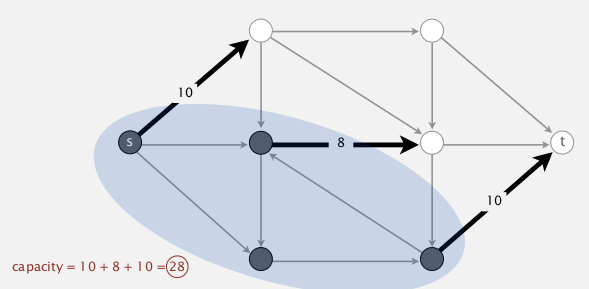
⇒ min-cut pb: find the cut (A,B) with min-capacity.

Max-flow pb

• same input: graph G, source s, target t
• def. an st-flow is an assignment of values to edges f: e→f[e] such that:
  • capacity constraint: 0<=f[e]<=c[e] for any e;
  • local equilibrium: for any vertex v (other than s or t), inflow=outflow;
• def. the value of a flow f is the inflow at t. (assume no ingoing edge to s or outgoing edge to t)

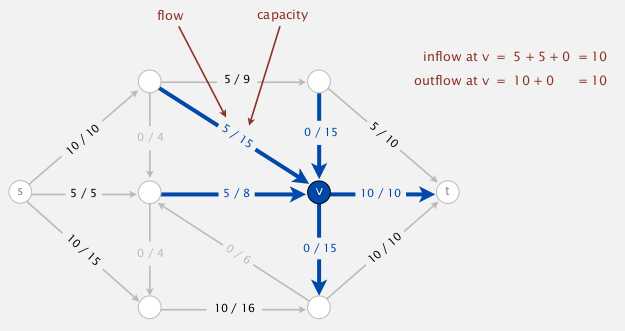
⇒ max-flow pb: find f with max value.

remark: max-flow and min-cut are dual problems.

2. Ford-Fulkerson Algorithm

def. given a flow f for a graph, an "augment path" is an undirected path form s to t, if there exist df>0 ("bottleneck capacity") such that:

• for forward edges e: can augment flow by df (not full: f[e]+df<=c[e])
• for backward edges: can decrease flow by df (not empty: f[e]-df>=0)

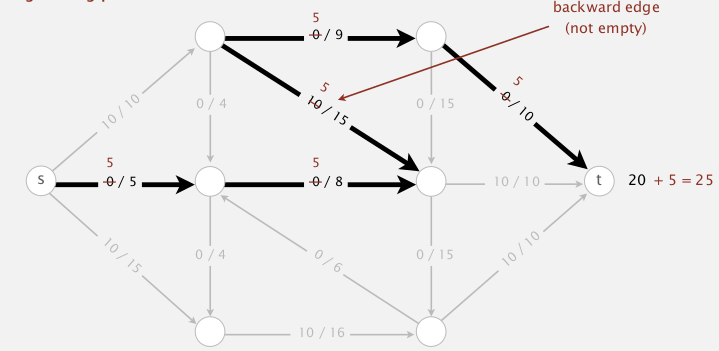
• def. residual capacity
  • for forward edge e, residual-cap = c[e]-f[e]
  • for backward edge e, residual-cap = f[e]

⇒ an aug-path is a path where each edge has residual capacity >0.

blocking edges: full forward edge or empty backward edge.

→ idea: increase flow along augment paths.
[algo]

• start: 0 flow: f[e]=0 for all e.
• find an augment path (and the corresponding df) in graph, and change the flows along the path by +/-df.
• loop until no augment path exists. (ie. all path s→t are blocked either by a full forward edge or an empty backward edge, ie. by an edge with 0 residual capacity)

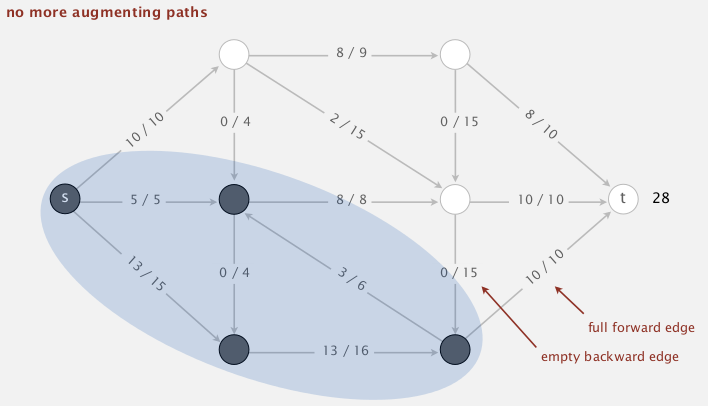
FF is a gernel algorithm:

3. Maxflow-Mincut Theorem

def. for a cut (A,B), the net flow across the cut (netflow(A,B)) is the sum of flows from A to B minus flows from B to A.

[flow-value Lemma]
For any flow f and any cut (A,B)⇒ netflow(A,B) = value(f).
pf.
induction on the size of set B.
base case, when B={t}, by def we have netflow(A,B) = value(f)
when moving any vertex v from A to B:
* netflow(A, B) augment by flow(A→v)+flow(B→v)=inflow(v),
* netflow(A, B) decrease by flow(v→A)+flow(v→B)=outflow(v),
* by equilibrium of flow, netflow(A',B')=netflow(A,B)=value(f)

ex. (A: gray vertices, B: white vertices)

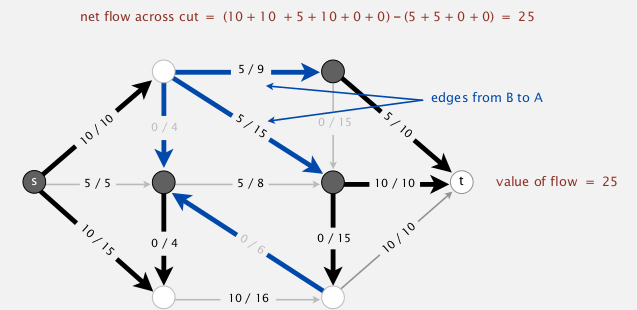
[cor] outflow(s)=inflow(t)=value(f)

[weak duality]
For any flow f and any cut (A,B), ⇒ value(f) <= capacity(A,B).

[Augmenting path Th]
A flow f is maxflow iff there is no augment path.

[maxflow-mincut Th]
value(maxflow) = capacity(mincut).

pf.
for any flow f, prove the equivalence of the 3 following statements:
i. there exists a cut st: capacity(cut) = value(f).
ii. f is a maxflow.
iii. there is no augmenting path wrt f.

• [i⇒ii]

suppose cut(A,B) st: capacity(A,B)=value(f)
⇒ by weak duality, for any other flow f', vlaue(f')<=capacity(A,B)=value(f)

• [ii⇒iii] (eqv to prove ~iii⇒~ii)

suppose there is an aug-path from s to t, of bottleneck capacity=df,
⇒ by improving f with df, we get a f' > f

• [iii⇒i]

suppose there is no aug-path, ie, all path from s to t are blocked by some full-forward edge or empty backward edge.
⇒ let A:=vertices connected with s by a path with no blocking edges, and B := the rest
(so once we get a maxflow, we can compute the mincut in this way)

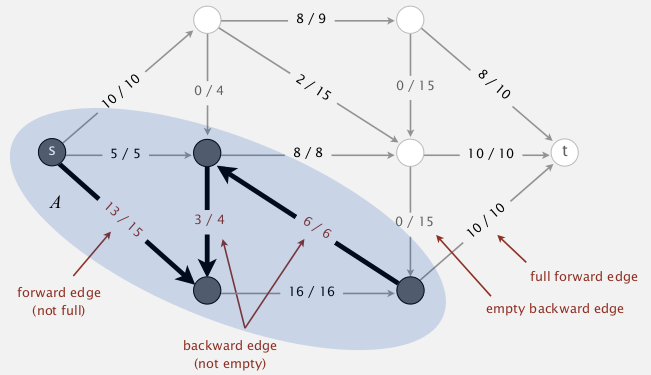
→ for all edges across A and B, all forward edges are full, all backward edges are empty
⇒ capacity(A,B) = netflow(A,B) = value(f) by flow-value lemma
CQFD... 过瘾...

4. Running Time Analysis

• getting a mincut form maxflow? → easy (as discussed in the pf above)
• computing an aug-path? → BFS
• does FF algo always terminate? how many augmentations? → ...

integer capacity graphs

special case of FF algo: edge capacities are integers between 1 and U.

invariant: flow is always integer all along FF algo.

[prop] nb of augmentations <= value of maxflow.
pf. each augmentation will add flow by >=1.

[integrality Th] There exist an integer-valued maxflow.

Bad case for FF

nb of augmentation == value of maxflow
(each time, the path through the middle edge is chosen as aug-path)

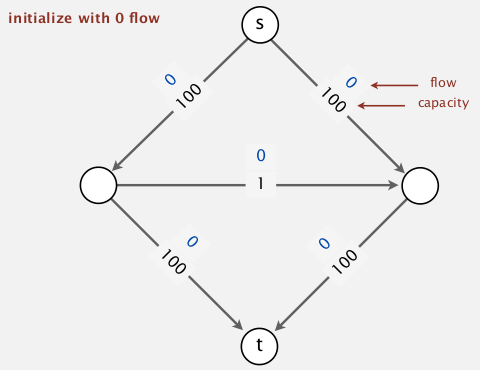
can be easily avoided⇒ by using shortest(nb of edges)/fastest(biggest df) path

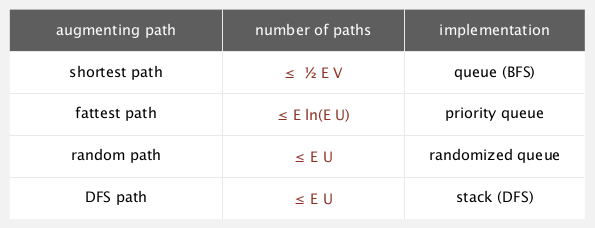
Performance of FF depends on the algo for choosing aug-path:

5. Java Implementation

representation of flow graph

• flow edge:

each e= v→w, have flow f[e] and capacity c[e].

• flow graph:

put e in both v and w's adj-list.

• flow augmentation (by delta)
  • for forward edge e, f[e] += delta
  • for backward edge e, f[e] -= delta

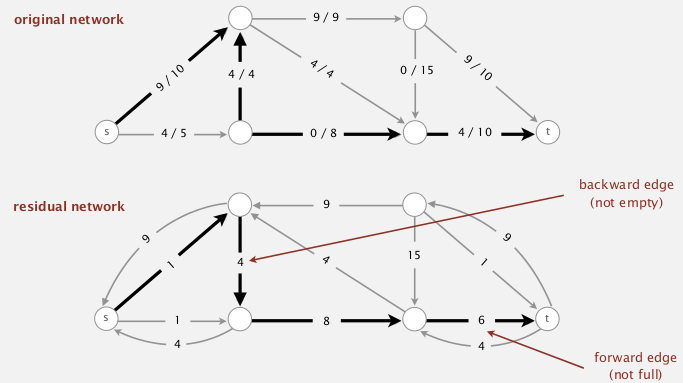
Residual graph Gr

def. For a flow f and a graph G, the residual graph Gr is obtained by:

for each edge e=v→w, (with c[e] and f[e]) in G, put in Gr:
e1=v→w, with weight=c[e]-f[e]
e2=w→v, with weight=f[e] (即两个方向上的weight都为residual capacity)

(rmq: Gr is just a weighted digraph, not a flow graph)

[prop] Augment path in G is equivalent to a path in Gr (df of aug-path in G = min edge weight in Gr).
(但是实现的时候其实不用显式构造Gr, 只需BFS的时候修改一下即可)

APIs

这里的API设计的非常合理... 导致每一部分的代码量都不大... NB

• flow-edge:
  rmq. both calculate residual-cap and augmentation need to specify a direction, so we need a index v as parameter for these 2 functions.

  public class FlowEdge{   
      private final int v, w;   
      private final double capacity;   
      private double flow=0.0;   
      FlowEdge(int v, int w, double cap);   
      int from();   
      int to();   
      int other(int v);   
      double capacity();   
      double flow();   
      double residualCapTo(int v);// residual capacity   
      void addFlowTo(int v, double delta);// augment residual flow   
  }
  

• flow graph:

  public class FlowNetwork{   
      private Bag<FlowEdge>[] adj;//use adj-list representation for flow graph   
      FlowNetwork(int V);   
      void addEdge(FlowEdge e);   
      Iterable<FlowEdge> adj(int v);// both incoming and outgoing edges   
      ...   
  }
  

• FF algo:

  • use a function hasAugPath() to test termination
  • use a function bottleNeck() to get delta
  • if a augpath is found, use two arrays reached[] and edgeTo[] to get the augpath (find the path backwards).

code:

public class FordFulkerson{   
private boolean[] reached; //reached[v] indicates if a path s-->v exists in Gr, used in DFS   
private FlowEdge[] edgeTo;// edgeTo[v] = last edge on the path s-->v   
private double value=0.0;// value of flow   
public FordFulkerson(FlowNetwork G, int s, int t){   
    while(this.hasAugPath(G,s,t)){   
        double delta = this.bottleNeck();   
        for(int v=t; v!=s; v=edgeTo[v].other(v))   
            edgeTo[v].addFlowTo(v, delta);   
        this.value += delta;// each time the flow value augments by delta   
    }   
}   
private double bottleNeck(){//bottleneck-cap = min residual flow on the aut-path   
    double bottleneck = 9999999;   
    assert(reached[t]);// the aug-path should exsit   
    for(int v=t; v!=s; v = edgeTo[v].other(v))   
        bottleneck = Math.min(bottleneck, edgeTo[v].);   
    return bottleneck;   
}   
private boolean hasAugPath(FlowNetwork G, int s, int t){   
    // perform a BFS    
    Queue<Integer> q = new LinkedList<Integer>();   
    this.reached = new boolean[G.V()];   
    this.edgeTo = new FlowEdge[G.V()];   
    q.add(s);   
    while(!q.isEmpty()){   
        int v = q.deque();   
        for(FlowEdge e:G.adj(v)){   
            int w = e.other(v);   
            if(!reached[w] && e.residualCapTo(w)>0){// modified BFS: valid edges are those with  residualCap>0   
                edgeTo[w] = e;   
                reached[w] = true;   
                if(w==t) return true;// t is reached by BFS  
                q.enqueue(w);   
            }   
        }   
    }// BFS while loop    
    return false;   
}   
}//class FF

6. Maxflow Applications

关键是建模很巧妙...

ex1. bipartite matching pb

二分图的最大匹配问题. (有点像marriage stable问题...但是不一样 因为没有preference order)

⇒ is there a way to match all students to a job?
ie. given a bipartite graph, find a perfect matching.

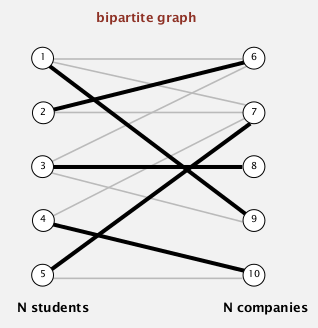
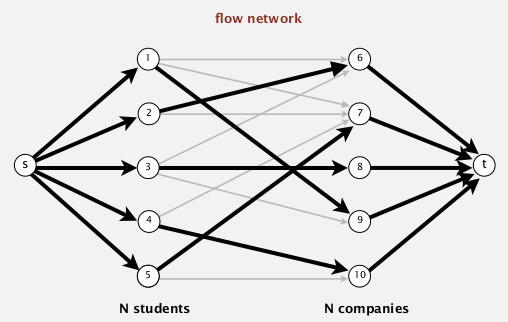
modeling

• add source s and target t
• all edges from s to students: capacity=1
• all edges from companies to t: capacity=1
• all edges from student to company: capacity=INF

⇒ find maxflow in the graph

when no perfect matching: mincut can explain why

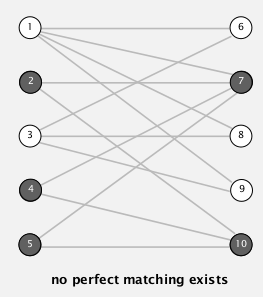
in the above case, student 2,4,5 can only be matched to 7,10
⇒ mincut can help us find such cases!

recall: how to get mincut from maxflow

mincut = (A,B), where:
A:=vertices connected with s by a path with non blocking edges,
B := the rest
(blocking edges: full forward edge or empty backward edge on path)

ex.

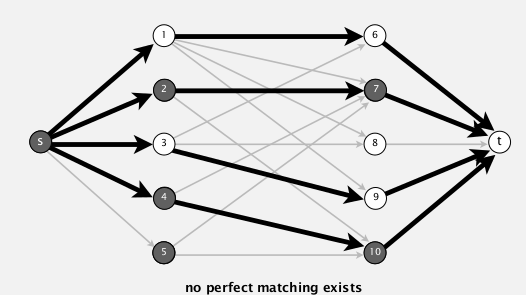
• let S=students on s side of mincut (in above case, S={2,4,5})
• let T=companies on s side of mincut (in above case, T={7,10})
• |S|>|T|, that's why no perfect matching!

ex2. baseball elimination

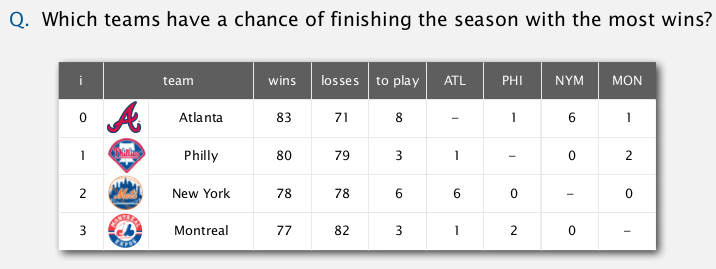
(前三列是目前成绩, 后面四列是接下来赛程矩阵)
Montreal is mathematically eliminated → easy to see
→ Philly is mathematically eliminated also !

• another case:

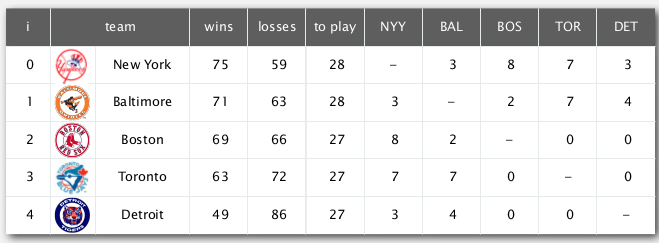
Detroit is mathematically eliminated !

whether team-4 still has a chance to win?
modelling

• remaining games flow from s to t.
• use team-pairs ans teams as vertices
• carefully chosen capacities(see below)

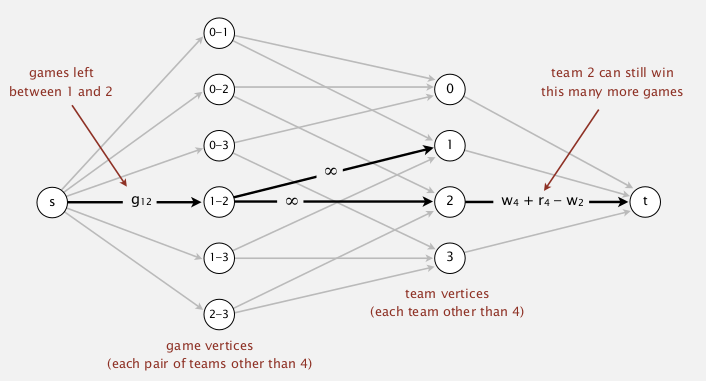
⇒ team 4 could win iff all flow from s are full (ie. all match points can be repartitioned over other teams without depassing team 4's maximum wins).
总之很巧妙....