1. Intro to graphs
Graph: vertices connected by edges.
terminology:
- path: sequence of vertices connected by edges
- cycle: path with same starting and ending vertex
- two vertices are connected: if there is a path between
ex of graph problems:
- path: or connectivity
- shortest path
- cycle
- Euler tour (ouii..)
- Hamilton tour
- MST
- bi-connectivity: is there a vertex whose removal disconnects the graph?
- planarity
- isomorphism
2. Graph API
graph representation
- vertex representation: use integers between 0 and V-1
- anormalies: self-loop and multiple edges are possible
public class Graph{ Graph(int V); void addEdge(int v, int w); Iterable<Integer> adj(int v); int V();// nb of vertices int E();// nb of edges }
print all edges:

basic functions:
static int degree(Graph g, int v){
int deg = 0;
for(int w:G.adj(v)) deg++;
return deg;
}
static int nbOfSelfloops(Graph g){
int cnt = 0;
for(int v=0; v<G.V(); v++)
for(int w:G.adj(v))
if (w==v) cnt++;
return cnt/2;
}
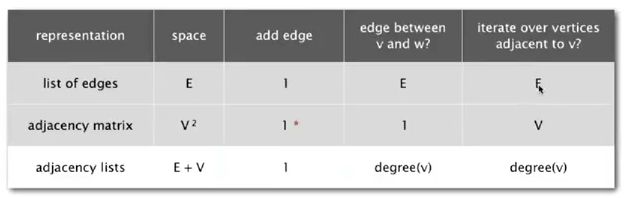
edge representation
- set-of-edge implementation: a list of all edges ⇒ can lead to inefficient implementation
- adj-matrix implementation: maintain a 2d (V*V) boolean array ⇒ space complexity too heavy
- adj-list implementation: vertex-indexed array, each array entry is a
Bag(类似桶bucket) ⇒ sutable for sparse graphs

adj-list implementation:
private final int V;
private Bag<Integer>[] adj;
public Graph(int V){
this.V = V;
this.adj = (Bag<Integer>[]) new Bag[V];// java cannot create generic array
for(int v = 0; v<V; v++) adj[v] = new Bag<Integer>();
}
public addEdge(int v, int w){
adj[v].add(w);
adj[w].add(v);// if undirected graph
}
3. Depth-First Search
Tremaux maze exploration: trace back when no unvisited vertices availiable.
动画好看...
DFS goal: systematically search through a graph.
design pattern: decouple graph data and graph processing.
public class Paths{
Path(Graph G, int s);// graph G and source s
boolean hasPathTo(int v);
Iterable<Integer> pathTo(int v);
}
algo:

注意每次访问节点以前就将其mark.
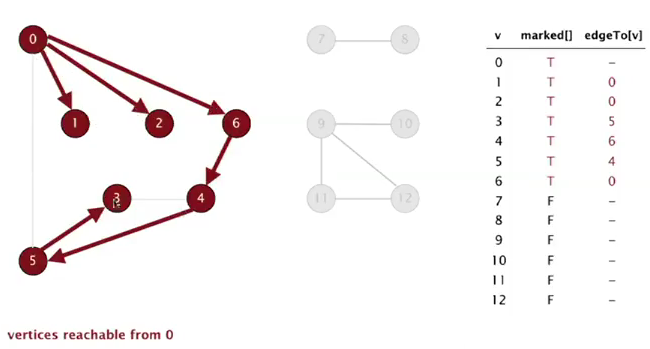
implementation
- 用一个boolean数组
visited[]作为标记 - 为了找到一条具体的路径(ie, 一系列节点), 维护一个
prev[]数组, 存放当前节点是从哪个节点走过来的.
//public class DFSpaths extends Paths...
boolean[] visited = new boolean[V];
int[] prev = new int[V];
public void dfs(int v){
visited[v] = true;
for(int w: G.adj())
if(!visited[w]) {
prev[w]=v;
dfs(w);
}
}
public Iterable<Integer> pathTo(int v){
Stack<Integer> s = new Stack<Integer>();
for(int x = v; x!=s; x = prev[x])
s.push(x);
return s;
}
properties
prop.
DFS visite all edges in time propotional to the sum of their degrees(ie. nb of edges).
4. Breadth-First Search
not recursive algo.
maintain a queue, add to queue for all vertices not-marked.
implementation
- use
visited[]to mark vertices - use a
prev[]array to get explicit path - use a
dist[]array to record the shortest dist from v to source (can usedistto replacevisited)public void bfs(Graph G, int s){ boolean visited[] = new boolean[G.V()]; int prev[] = new int[G.V()]; int dist[] = new int[G.V()]; Queue<Integer> q = new Queue<Integer>(); visited[s] = true; q.push(s); while(!q.isEmpty()){ int v = q.dequeue(); for(int w:G.adj(v)) if(!visited[w]) { prev[w] = v; visited[w] = true; q.enqueue(w); } } }
property
prop.
BFS computes the shortest path from s to all vertices using time propotional to E+V.
intuition: BFS examines nodes by increasing distance
5. Connected Components
dealing with connectivity(equivalence) queries ⇒ answer in constant time (with preprocessing).
public class CC{
boolean connected(int v, int w);
int count();// nb of CCs
int id(int v);//id for a CC
}
⇒ Union-Find ? ⇒ Use DFS!!
def. connected component is a maximal set of connected vertices.
algo: for each unmarked vertex, run dfs(with increasing cc id)...
after the preprocessing, we can get the array id[] and cc count cnt...
6. Graph Challenges
some typical pbs
pb1. bipartite graph
Can we divide vertices into 2 subsets, where all edge go from one subset to other.
⇒ can be done with dfs. cf. booksite
pb2. cycle detection
⇒ simple using dfs.
pb3. Euler cycle
Find a cycle that uses all edges exactely once.
[Euler] a graph is Eulerian iff all vertices have even degree.
⇒ typical diligent algo students can do. cf. booksite
pb4. Hamilton cycle
Find cycle that visits each vertex exactly once.
⇒ intractable (typical NP-complete pb)
pb5. isomorphism of graphs
Are two graphs identical except for vertex names?
⇒ no one knows...
pb6. planary graph
Lay out a graph in the plane without crossing edges?
⇒ expert level. exists linear time algo based on DFS by Tarjan, but too complicated.
Part 1 of series «Algorithms Princeton MOOC II»:
- [Algorithms II] Week 1-1 Undirected Graphs
- [Algorithms II] Week 1-2 Directed Graphs
- [Algorithms II] Week 2-1 Minimum Spanning Trees
- [Algorithms II] Week 2-2 Shortest Paths
- [Algorithms II] Week 3-1 Maximum Flow
- [Algorithms II] Week 3-2 Radix Sorts
- [Algorithms II] Week 4-1 Tries
- [Algorithms II] Week 4-2 Substring Search
- [Algorithms II] Week 5-1 Regular Expressions
- [Algorithms II] Week 5-2 Data Compression
- [Algorithms II] Week 6-1 Reductions
- [Algorithms II] Week 6-2 Linear Programming
- [Algorithms II] Week 6-3 Intractability
Disqus 留言