1. Introduction to MSTs

Given: undirected connecte graph G with positive edge weights.
def. Spanning tree T
is a subgraph of G, that is both tree (connected, acyclic) and spanning(all vertices are included).

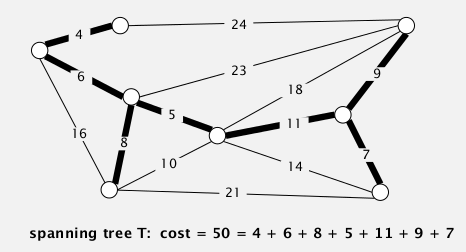
⇒ Goal: find a spanning tree with minimum weight sum.

2. Greedy Algorithm

assumptions for simplification:

• edge weights are distinct
• graph is connected

→ MST uniquely exists.

cut property

def. a cut of a graph is a partition of its vertices into 2 non-empty sets.
def. a crossing-edge (wrt a cut) is an edge connecting vertex from one set to another.

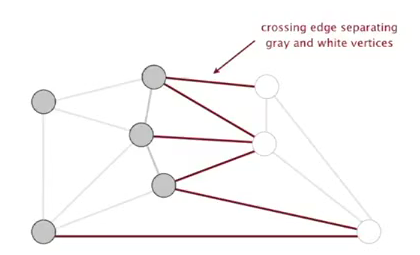
prop. Given any cut, the crossing edges with minimum weight is in the MST.

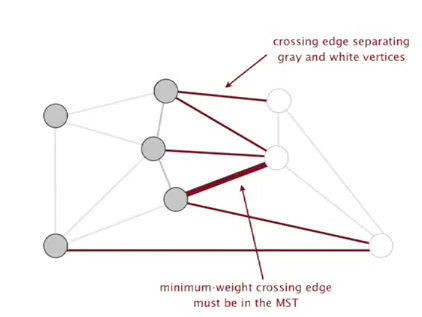
proof.
Given a cut. {S1,S2} are the two set of vertices, let e be the min-weighted edge among all crossing-edges.

If e is not in the MST
→ exist another crossing-edge, f, in the MST (otherwise not connected)
→ adding e to the MST will create a cycle (tree property)
→ the edge f will be in this cycle
→ removing f and adding e will give us another spanning tree (!)
→ this new spanning tree has smaller weight sum ⇒ contradiction, CQFD.

Greedy MST algo

[algo ] Greedy MST

• initialize: all edges not selected (colored gray)
• find any cut with all crossing-edge gray
• use this cut and select the min-weighted crossing edge (color the edge as black)
• repeat V-1 times.

prop. the greedy algorithm gets the MST.
pf.

• any selected (black) edges are in the MST (according to the cut property)
• If we haven't selected V-1 edges → there is always a cut with all crossing-edges gray. (证明algo不会卡死)

(if edge weight not distinct, the proof fails, but can be fixed)

efficient implementations:

• how to choose the cut each time?
• how to find min-weighted crossing-edge?

⇒ Kruskal & Prim

3. Edge-Weighted Graph API

Edge API

→ Edge abstraction: make Edge comparable.

public class Edge implements Comparable<Edge>{   
    Edge(int v, int w, double weight);   
    int either();// get one of the endpoint of edge (as we are in undirected graph contex here)   
    int other(int v);// get the other endpoint    
    int compareTo(Edge that);// compare by edge weight   
    double weight();   
}

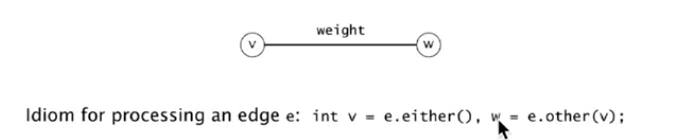
Edge-weighted Graph API

adj-list implementation: Bag<Edge>[] adj;(for undirected graph, each edge appears twice in adj)

public class EdgeWeightedGraph{   
    private final int V;   
    private final Bag<Edge>[] adj;   
    EdgeWeightedGraph(int V){   
        this.V = V;   
        this.adj = (Bag<Edge>)new Bag[V];   
        for(int v=0;v<V;v++) adj[v] = new Bag<Edge>();   
    }   
    void addEdge(Edge e){// use the Edge class instead of directly v and w   
        int v = e.either(), w = e.other();   
        adj[v].add(e);   
        adj[w].add(e);   
    }   
    Iterable<Edge> adj(int v){//get Edges incident to v   
        return adj[v];   
    }   
    Iterable<Edge> edges();// get all Edges   
}

(allow self-loops and parallel edges)

MST API

public class MST{   
    MST(EdgeWeightedGraph G);//compute the MST   
    Iterable<Edge> edges();// selected edges in the MST   
    double weight();// sum of all edge weights in MST   
}

4. Kruskal's Algorithm

[algo]

• consider edges in ascending order of weight,
• add the edge to MST unless it creates a cycle.

In the running of Kruskal: we have several small connect components and they merge with each other until we get MST.

correctness

prop. Kruskal's algo works.
pf
(idea: proove that Kruskal is a special case of the greedy algorithm, ie. how to select the specific cut)
suppose Kruskal's algo selects(colored black) an edge e=v-w
→ select a cut = vertices connected to v in the (constructing) MST; and the rest vertices.
→ for this cut, there is no black crossing edges
→ moreover among all crossing edges of the cut the edge e has the smallest weight!! (by def of Kruskal) CQFD

implementation

• how to test if adding an edge will create a cycle ?

DFS from v to w? → O(V)
⇒ Union-Find ! O(lg*V) ☺ (almost constant time)

if find(v)==find(w), then we know adding e will create a cycle.

• considering edges in order? → use a prority queue.

  public class KruskalMST extends MST{   
      private Bag<Edge> mst = new Bag<Edge>();   
      public KruskalMST(EdgeWeightedGraph G){   
          MinPQ<Edge> pq = new MinPQ<Edge>();   
          // build pq --> can be optimized to O(n) if build bottom-up   
          for(Edge e: G.edges()) pq.insert(e);   
          UF uf = new UF(G.V());// build a UF of V elements   
          while(!pq.isEmpty() && mst.size()<G.V()-1){   
              Edge e = pq.delMin();   
              int v = e.either(),w=e.other(v);   
              if( uf.connecte(v,w) ) continue;   
              uf.union(v,w);   
              this.mst.add(e);           
          }   
      }   
      public Iterable<Edge> edges(){   
          return this.mst;   
      }   
  }
  

complexity

running time: O(ElogE)

5. Prim's Algorithm

since 1930...
Idea: start from a vertex and grows the tree T to MST.

[algo]

• Add to the tree T the edge that have exactely one endpoint in T and with minimum weight,
• repeat V-1 times.

In the running of Prim: there is always ONE connnected component .

Correctness

prop. Prim's algo works.
pf.
suppose edge e is the min-weighted edge connect a vertex in T with a vertex out of T.
→ select the cut = vertices in the tree T; vertices out of T
→ by def, there is no black crossing edge
→ e is the min-weighed edge by def of Prim. CQFD

implementation

challenge: how to find such an edge (connect T and other vertex, with min weight) ?
⇒ priority queue

"lazy" implementation

[algo]

• Maintain a PQ of edges that connect T and the rest vertices.
• e = pq.delMin(), e = v-w, if v and w are both in T (as edges in pq might become obsolete as T grows) ⇒ just disregard it
• to maintain the pq: add all incident edges(with other endpoint not in T) of the newly added vertex to pq

public class LazyPrimMST{   
    private Bag<Edge> mst;   
    LazyPrimMST(EdgeWeightedGraph G){   
        boolean[] marked = new boolean[G.V()]; // vertices in T   
        MinPQ<Edge> pq = new MinPQ<Edge>();    
        this.mst = new Bag<Edge>();   
        marked[0] = 0; // add vertex 0 to T   
        for(Edge e:G.adj(0))    
            pq.insert(e);// add edges to pq   
        while(!pq.isEmpty() && this.mst.size()<G.V()-1){   
            e = pq.delMin();   
            int v = e.either(), w = e.other(v);   
            if(marked[v] && marked[w]) continue;//ignore obsolete edges   
            v = marked[v] ? w : v;// v is the newly added vertex   
            marked[v] = true;   
            for(Edge e:G.adj(v)){   
                if(!marked[e.other(v)])   
                    pq.insert(e);   
            }   
        }   
    }   
}

Running time: O(ElgE)

space: O(E) in worst time.

"eager" implementation

Idea:

use a PQ of vertices, priority of vertex v := min-weight of edge that connects v to T.

[algo]

• Get from pq the vertex v that is closest to T, add it to T.
  Update pq -- consider v's incident edge e=v-w:
  • if w in T → ignore
  • else:
    • if w in pq → add w to pq
    • else → if v-w has smaller weight than the current priority, update w's priority.
• repeat till get V-1 edges.

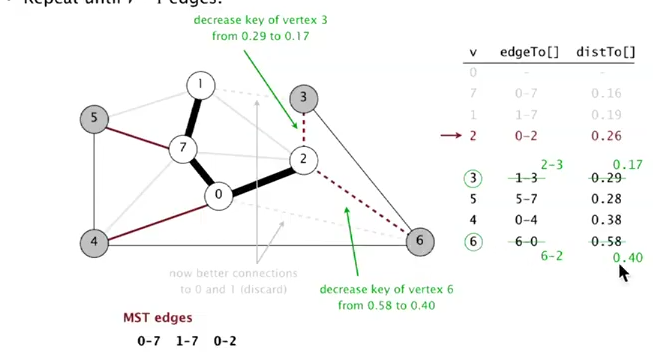
key implementation component: a MinPQ that supports priority(key) update.

class IndexMinPQ<Key extends Comparable<Key>>{   
    IndexMinPQ(int N);// indices of elements: 0...N-1   
    void insert(int i, Key key);   
    void decreaseKey(int i, Key key);// update the key(priority) of element-i   
    int delMin();   
    int size();   
}

implementation of such a PQ:

Use same code as standart PQ (maintain a heap[] array).
Elements are always accessed by "index", in range 0...N-1. maintain 3 parallel arrays: keys[], pq[], qp[]:

• keys[i]: is the priority of element i (the element with index=i)
• pq[i]: is the index of the element in the heap position i (ie. in heap[i] is pq[i]th element )
• qp[i]: is heap position of element i ( ⇔ the ith element is in heap[qp[i]] )

to decreaseKey(i,key): change keys[i], then call siftup(qp[i])

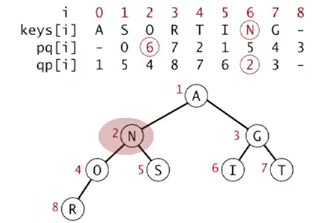
summery of pq implementations:

6. MST Context

• unsolved pb: does a linear MST algo exists?

(recap: for UF, tarjan has prooved that linear algo doesn't exist — although Nlg*N is fast enough...)
@_@...

(这个Yao是清华那个Yao吧?)

• Euclidean MST

Given N points in plane, edge weight := Euclidean distance. (dense graph, E = V2)
→ exploit geomerty, O(NlgN)

• clustering

k-clustering (~ dist-fcn)
single-link clustering (def. dist of clusters = dist of 2 closest elements in each cluster)
→ Kruskal...