[Scala MOOC I] Lec4: Types and Pattern Matching

4.1 - Objects Everywhere

scala is pure OO: every value is an obj, every operation is a method of obj.

scala.Int scala.Boolean maps to JVM standard primitive types.

Implement Boolean withous primitive type in scala:

Then defin false and true as objects, give implementation for ifThenElse() funciton:

object true extends Boolean{ 
    def ifThenElse[T](t: =>T, e: =>T) = t 
} 
object false extends Boolean{ 
    def ifThenElse[T](t: =>T, e: =>T) = e 
}

4.2 - Functions as Objects

Function values are treated as objects in scala.
the type A => B is an abbrevation for scala.Function1[A, B]

Functions are objects with apply methods.

anonymous function (x: Int) => x*x is expanded to :

new Function1[Int, Int]{ 
def apply(x: Int) = x*x 
}

function call f(a,b) is expanded to: f.apply(a,b) List(1,2) is expanded to : List.apply(1,2)

4.3 - Subtyping and Generics

2 forms of polymorphism: subtyping and generics

Type Bounds

assertAllPos taks either EmptySet or NonEmptySet, the return type is EmptySet (when para=EmptySet) or NonEmptySet (when para=NonEmpty).
To express this situation:

def assertAllPos[S <: IntSet](r: S): S = ...

Here <: IntSet means IntSet is an upper bound of the type parameter.

and we can mix the two notations:

[S >: NonEmpty <: IntSet]

Covariance

Given NonEmpty <: IntSet,
should we have: List[NonEmpty] <: List[IntSet] ?

In this case the typse are called *covariant. *

In java, arrays are covariant: NonEmpty[] <: IntSet[] but this might cause problems:

will get ArrayStoreException in 3rd line.

Liskov substitution principle: when a type can be a subtype of another

If A<:B, then everything one can do with an object of type B, one should also be able to do it with object of type A.

In scala the Array is not covariant: Array[IntSet] is not supertype of Array[NonEmpty]

4.5 - Decomposition

ex: arithmetic expression interpreter: a tree of numbers and sums, both are subtype of Expr.

1st try: test and accessor methods

→ tedious... And to add more operands need to add many more methods...

2nd try: (non-solution) type testing and type casting isinstantceof, asinstanceof

discouraged in scala.

1st solution: OO decomposition add eval method to class Expr.

limitation: if we want to simplify an expression,

⇒ there is no local simplification !

⇒ pattern matching

4.6 - Pattern Matching

goal: reverse the construction process.

• which subclass it is?
• what were the arguments?

case classes

add case in class definition. ex.

case class Number(n: Int) extends Expr 
case class Sum(e1: Expr, e2: Expr) extends Expr

adding case adds companion objects with apply methods:

according to the expansion, Number(2) is equal to Number.apply(2) which is actaully new Numver(2)

pattern matching

match: extension of switch in java, ex:

def eval(e: Expr): Int = e match{ 
    case Number(n) => n 
    case Sum(e1, e2) => e1 + e2 
}

patterns include:

• constructor, ex. Number(n)
• variable, ex. n, e1, e2
• wildcard patters, ex. _
• constant, ex. 1, true
• or their combination, ex Sum(Number(1), Var(x))

The whole match expression is replaced with the expression to the rhs of the first match pattern.

exercice: implement a show function.

def show(e: Expr): String = e match { 
    case Number(n) => n.toString 
    case Sum(l, r) => show(l) + "+" + show(r) 
}

4.7 - Lists

example:

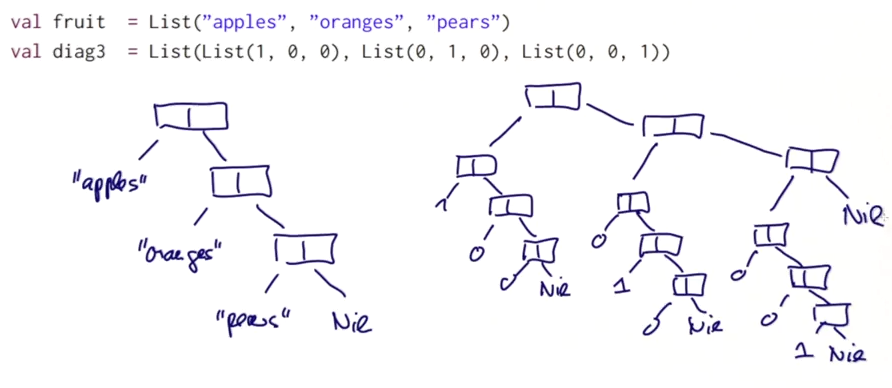
difference between List and Array:

• Lists are immutable, elements cannot change
• Lists are recursive, arrays are flat
• both are homogeneous, all elements of the same type

All Lists in scala are constructed with:

• Empty list Nil
• construction op ::(pronunced: cons), x::xs

convention in scala: operators ending with :

• are right-associative. a::b::c is equal to a::(b::c)
• seen as method calls from the right-hand operand. 1::2::Nil equal to Nil.::(2).::(1) ( :: is prepend operation)

operations on lists:

• head
• tail
• isEmpty

list in pattern matching:

ex. insertion sort of lists

def isort(xs: List[Int]): List[Int] = xs match{ 
    case List() => List() 
    case y::ys => insert(y, isort(ys)) 
} 
def insert(x:Int, xs:List[Int]): List[Int] = xs match{ 
    case List() => List(x) 
    case y::ys => if(x<=y) x::xs else y::insert(y, ys) 
}