1. Introduction to Intractability

recall model of computation: DFA
a univeral model of computation: turing machine
→ no more powerful model of computation.
Turing machine can compute any function that can be computed by a physically harnessable process of the natural world.

bottom line: turing machine is a simple and universal model of computation.

Q. which algos are useful in practice?

useful in practice = polynomial time for all inputs

def. a pb is intractable if it cannot be solved in polynomial time.

2 pbs that can be proved to require exp time:

1. Given a constant-size programme, does it halt in <=K steps ?
2. Given a N*N chess board position, can the first player force a win ?

Bad news: very few pbs can be proved to require exp time...

2. Search Problems

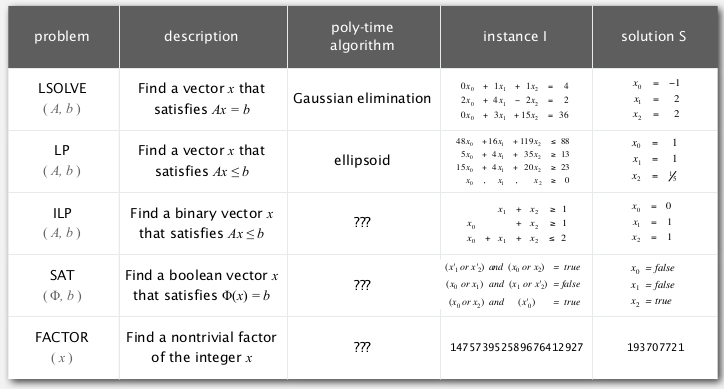
Four fundamental problems:

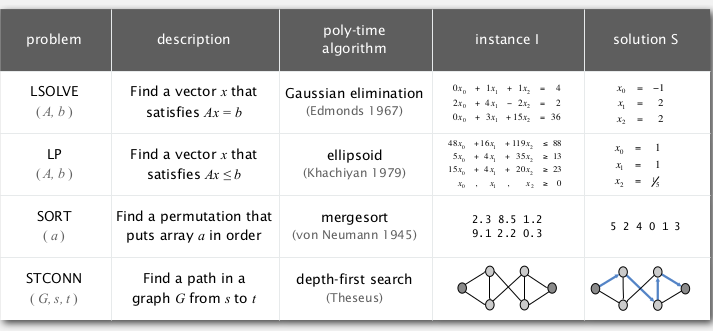
• LSLOVE

Given a system of linear equations, find a solution
var: real numbers
→ guassian elimination

• LP

Given a system of linear inequaties, find a solution. (not necessarily find the opt)
var: real numbers

• ILP

Given a system of linear inequaties, find a 0-1 solution.
var: 0 or 1

• SAT

Given a system of boolean equations, find a binary solution.

Which ones of the 4 foundamental pbs have poly-time solutions?

• LSLOVE: Gaussian elimination works in O(n3)
• LP: Ellipsoid works in poly-time (simplex also poly-time in practice..)
• ILP, SAT: No poly-time algorithm known (or believed to exist) !

All 4 pbs are examples of search problems.

Search pb: given an instance I, find a solution S / report there's no solution.
requirement: able to efficiently (poly-time) check that S is a solution. (that's the case for the above 4 fundamental pbs)

another example:
FACTOR: given a n-bit integer, find a nontrival factor.
(given a solution, simply need to long-divide to check...)

3. P vs. NP

def. NP is the class of all search pbs. (ie. solution be checked efficiently)
NB: classical definition limits to yes-no pbs...
Significance: NP pbs are what scientists and engineers aspire to compute feasibly.
examples:

def. P is the class of search pbs that are solvable in poly-time.

(What scientists and engineers do compute feasibly.)

examples:

Nondeterminism
Nondeterminism machine can guess the solution (donot exist in natural world..). → NFA tries to simulate such a machine...
Ex. int[] a = new int[N];
・ Java: initializes entries to 0 .
・ Nondeterministic machine: initializes entries to the solution!

NP: Search problems solvable in poly time on a nondeterministic Turing machine.

Extended Church-Turing thesis:
P: Search pbs solvable in poly time in natural world.

do we have non-determinism in natural world? ---> natural computers ?
ex. STEINER tree: set of segments connecting given N points.
use soap → doesn't really work...

another example for P/NP: automating creativity
being creative VS appreciating creativity

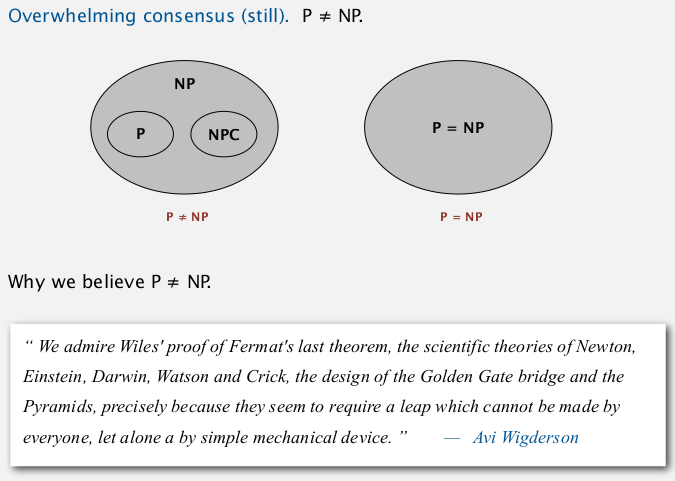
The central question: does P=NP?
(can you alway avoid brute-force searching and do better?)

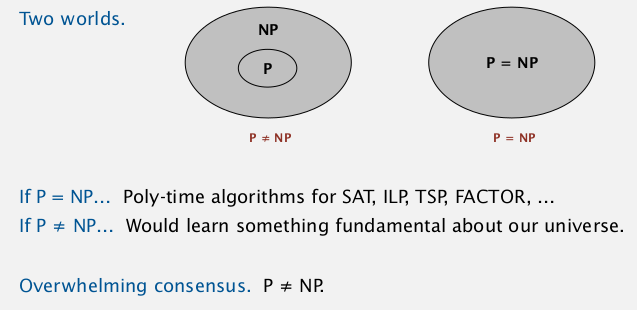
Millennium prize by Clay instute.
(among all ways of earning 1M dollars, this might be the most complicated way... @_@...)

4. Classifying Problems

classify pbs like classifying elements into perodic table.

key pb: satisfiablity
SAT. given a sys of boolean eq, find a solution.

exhaustive search: try 2^n possible solutions.
conjecture: no poly-time algo for SAT (ie. intractable)

Assumption: assume the intractability for SAT.
Tool: reduction
def. pb X reduces to pb Y: we can solve pb X with the algo for pb Y.

if SAT poly-reduces to pb Y ⇒ pb Y in (probably) intractable.

SAT poly-reduces to ILP

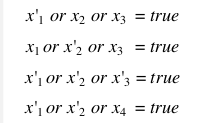
(all SAT pb can be reduced to 3SAT)

⇒ can be converted to an ILP pb:
for each eq, introduce a var Ci:

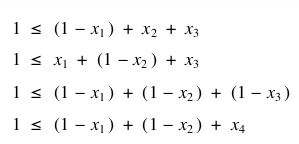
5. NP-Completeness

def. an NP pb is NP-complete if all pbs in NP poly-reduces to it.

prop. SAT id NP-complete.
any pb in NP poly-reduces to SAT (reverse direction as last lecture)
pf sketch: convert non-dertiministic turing machine notation to SAT notation...

cor. poly time algo for SAT iff P=NP...

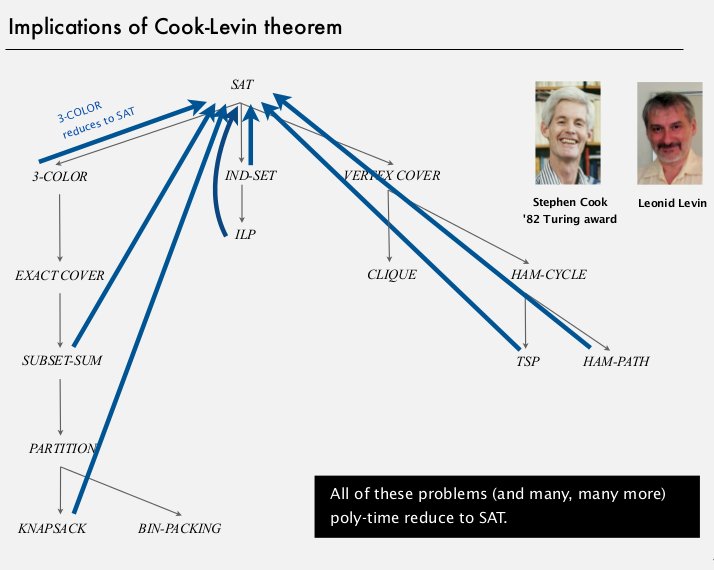
⇒ there pbs are equivalent !

summary:

==...

6. Coping with Intractability

exploit intractability

cryptography ecopoits the hardness of FACTOR pb

Can factor an n-bit integer in n 3 steps on a "quantum computer.”

Coping with intractability

relax one of desired features...

• special cases

• Develop a heuristic, and hope it produces a good solution.

no guarantee
ex. TSP

• Approximation algorithm. Find solution of provably good quality.

Halmiton path

remark: Euler path (each edge once) easy, Halmiton path (each vertex once) NPC...
dfs solution for Halmiton path:

public class Halmiton{   
    private boolean[] marked;   
    private int count=0; // nb of Halmiton paths   
    public Halmiton(Graph G){   
        marked = new boolean[G.V()];   
        for (int v=0; v<G.V(); v++)   
            dfs(G,1,1);    
    }   
    private void dfs(Graph G, int v, int depth){   
        if(depth==G.V()) count++;   
        marked[v]=true;   
        for(int w: G.adj(v))    
            if(marked[w]==false) dfs(G, w, depth+1);   
        marked[v]=flase; // backtrack   
    }   
}