1. Shortest Paths APIs

context: directe, weighted graphs.

shortest path variants

in terms of vertices:

• source-sink: form one vertex to another
• single source: from one vertex to all others (considered in this lecture)
• all pairs

constraints on edge weights:

• nonnegative weights
• arbitary weights
• eculidean

cycles:

• no directed cycles
• no negative cycles

APIs

for weighted directed edge:

public class DirectedEdge{   
    DirectedEdge(int v, int w, double weight);   
    int from();   
    int to();   
    double weight();   
}

for edge-weighted digraph:

public class EdgeWeightedDigraph{   
    private final Bag<DirectedEdge>[] adj;    
    EdgeWeightedDigraph(int V);   
    void addEdge(DirectedEdge e);   
    Iterable<DirectedEdge> adj(int v);   
    int V();   
}

for single source shortest-path:

public class SP{   
    SP(EdgeWeightedDigraph G, int s);//s is the source node   
    double distTo(int v);//dist from s to v   
    Iterable<DirectedEdge> pathTo(int v);// shortest path from s to v   
}

2. Shortest path properties

goal: single-source shortest path
prop. a shortest-path-tree (SPT) exists.
这个结论以前没见过... 不太evident吧... 没有太想明白

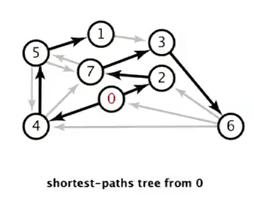
⇒ consequence: can represent this SPT by 2 vertex-indexted arrays:

• double distTo[v] = shortest path length s → v
• DirectedEdge edgeTo[v] = last edge to v in shortest path, edgeTo[s] = null

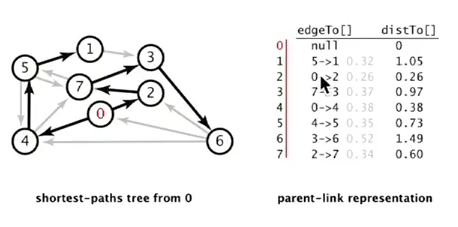
private int distTo[] = new int[V];   
private DirectedEdge edgeTo[] = new DirectedEdge[V];   
public double distTo(int v){   
    return this.distTo[v];   
}   
public Iterable<DirectedEdge> pathTo(int v){   
    Stack<DirectedEdge> path = new Stack<DirectedEdge>();   
    for(DirectedEdge e = this.edgeTo[v]; e!=null; e = edgeTo[e.from])   
        path.push(e);   
    return path;   
}

Edge relaxation

dynamic prog:

• distTo[v] = length of known shortest path from s to v
• distTo[w] = length of known shortest path from s to w
• edgeTo[w] = last edge in the known shortest path form s to w

(consider edges one by one)
def. edge e = v-->w relaxes if e.weight+distTo[v] < distTo[w]. → update distTo[w] and edgeTo[w].

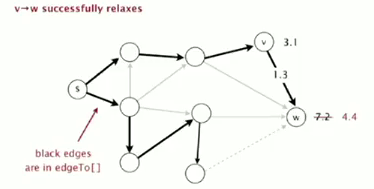
private void relax(DirectedEdge e){   
    int v = e.from(), w = e.to();   
    if(distTo[w]>distTo[v]+e.weight()){   
        distTo[w] = distTo[v]+e.weight();   
        edgeTo[w] = e;   
    }   
}

optimality conditions

prop. optimality conditions
distTo[] is the solution iff:

• distTo[s] = 0
• distTo[v] is the weight of some path from s to v
• for any edge e = v → w, distTo[w] <= distTo[v]+e.weight()

Generic algo

just relax all edges...

prop. the above generic algo gives the SPT from s.

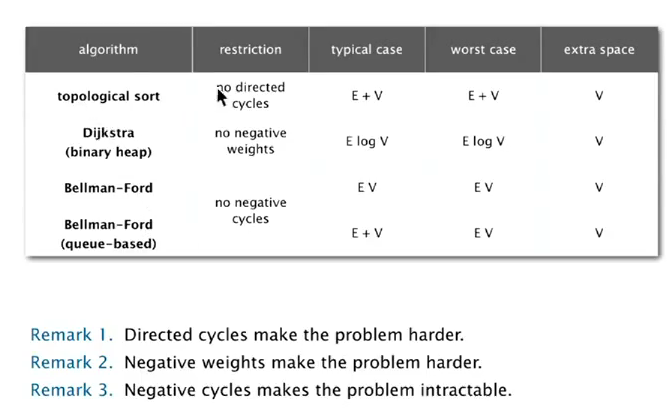
implementations of the algo:

• Dijkstra (nonnegative edge)
• Topological sort (!) (no directed cycles)
• Bellman-Ford (no negative directed cycles)

3. Dijkstra's Algorithm

(non-negative edges)

• consider vertices in increasing distance from s.*
• add vertex to the SPT, relax all edges from that vertex.
• each time: take the closest vertex to s that is not in the SPT (ie. whose dist is not determined yet), add the vertex, and relax all its outgoing edges.

prop. Dijkstra works.
pf.
each edge e = v → w is considered exactly once (when vertex v is added to SPT). distTo[w] <= distTo[v]+e.weight() after relaxing e
ineq holds until algo terminates
* distTo[w] decrease monotonely,
* distTo[v] will not change because each time we choose distTo[v] smallest, and all edges non-negative.
* CQFD by optimality condition.

implementation

Use an IndexMinPQ to store vertices.

public class DijkstraSP{   
    private int dist[];   
    private DirectedEdge edgeTo[];   
    private IndexMinPQ<Integer,Double> pq;   
    DijkstraSP(EdgeWeightedDigraph G, int s){   
        this.dist[] = new int[G.V()];   
        this.edgeTo[] = new DirectedEdge[G.V()];   
        this.pq = new IndexMinPQ<Integer,Double>(G.V());   
        for(int v = 0; v<G.V(); v++)  dist[v] = 999999;   
        dist[s] = 0;           
        pq.insert(s, 0.0);   
        while(!pq.isEmpty()){   
            int v = pq.delMin();   
            for(DirectedEdge e:G.adj(v))    
                relax(e);// decrease key or insert vertices to pq   
        }   
    }//constructor()

    private relax(DirectedEdge e){   
        int v = e.from(), w = e.to();   
        if(dist[w]<dist[v]+e.weight()){   
            dist[w] = dist[v]+e.weight();   
            edgeTo[w] = e;   
            if(pq.contains(w)) pq.decreaseKey(w, dist[w]);   
            else pq.insert(w, dist[w]);   
        }   
    }//relax()   
}//class

Dijkstra is in fact a Prim algorithm ! Both are algos that compute a spanning tree.

• in Prim: each time takes the vertex closest to the tree (and is for undirected graph).
• in Dijkstra: each time takes the vertex closest to source s (and is for directed graph).

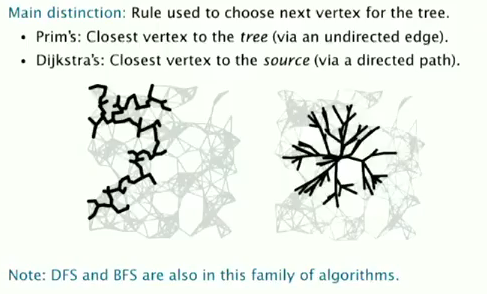
DFS BFS are also computing spanning tree!
...NB!!

complexity

• V insertions to PQ (each vertex is added to the SPT)
• V delMin from PQ
• E decrease key

→ depends on the PQ implementation.
in our implementation, O(ElogV)

4. Edge-Weighted DAGs

in a DAG, it's easier to find the shortest path ?
⇒ yes!
simple algo:

• consider vertices in topological order
• relax outgoing edges form this vertex.

correctness

prop.

topo-sort algo computes SPT in any DAG (even with negative weights) in time O(E+V) (linear time!).

pf.
each edge is relaxed exactely once. distTo[w] <= distTo[v]+e.weight() after relaxing e
ineq holds until the algo terminates because:
* distTo[w] decrease monotonely,
* distTo[v] will not change because of topo-order, no edge pointing to v after v is relaxed.
* CQFD

implementation

public class AsyclicSP{   
    AsyclicSP(EdgeWeightedDigraph G, int s){   
        // init dist[] and edgeTo[]...   
        Topological topo = new Topological(G);   
        for(int v: topo.order())   
            for(DirectedEdge e:G.adj(v))   
                relax(e);   
    }   
}

application

• seam-carving

Resizing images non-uniformly without distortion.

好神奇!
Grid DAG of pixels, edges are pointed to 3 downward neighbors.
横向缩小: 删掉一个"seam"

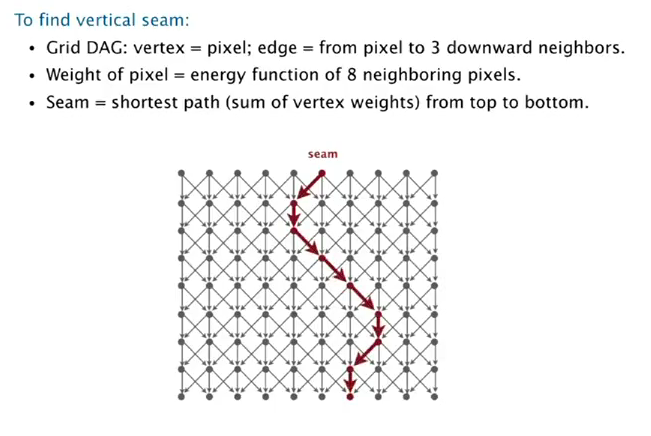
• longest path in DAG → just negate all edge weights, as this algo is OK for negative edges.

• parallel job scheduling
  
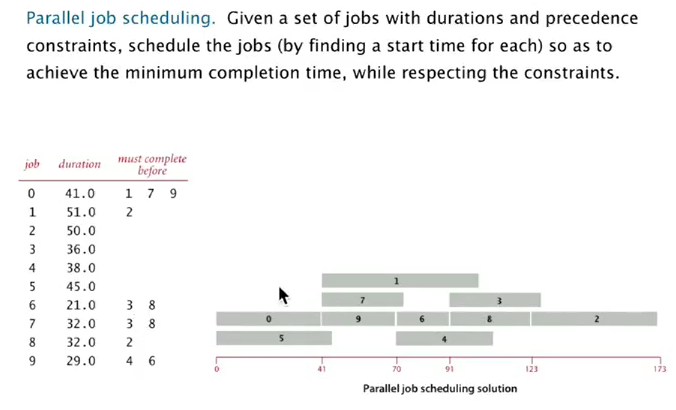
  感觉有点运筹的意思, 关键是建立一个DAG, 比较有技巧性:

  • add source and sink
  • split each job to 2 vertices (begin and end)

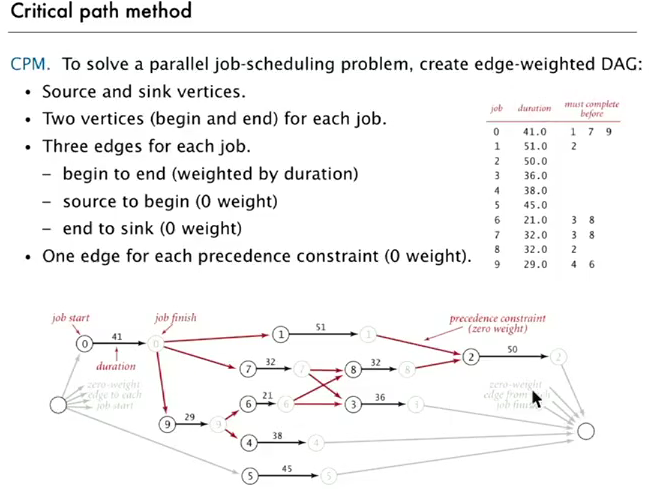
⇒ use longest path to schedule jobs

5. Negative Weights

只是给所有边增加weight并不能解决负权边问题.

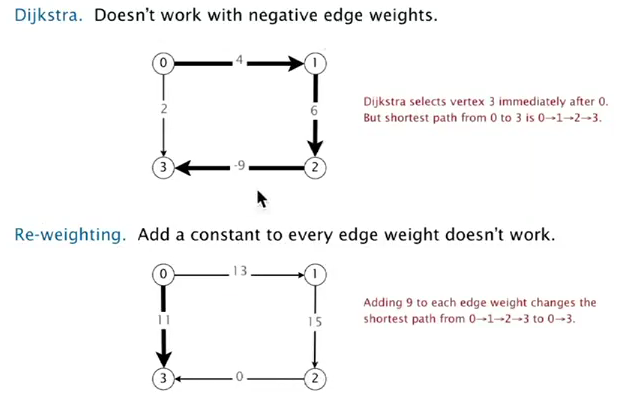
⇒ need a different algo.

prop. SPT exists iff there is no negative cycles.

Bellman-Ford

一句话总结Bellman算法: 每次relax所有的边, 进行V次.

(因为relax k次以后, s到v的最短路径的长度小于等于k.)

prop. Bellman-Ford works, complexity is O(EV).
pf.
after i passes, found shortest path contain at most i edges.

code:

public class BellmanFordSP{   
    BellmanFordSP(EdgeWeightedDigraph G, int s){   
        // init dist[] and edgeTo[]...   
        for(int i=0;i<G.V();i++)   
            for(DirectedEdge e:G.edges())   
                relax(e);   
    }

}

improvement

if dist[v] is not changed during one pasee → no need to relax incoming edges any more.
→ much faster in practice.

FIFO implementation: maintain a queue of vertices whoses dist is changed.

Finding negative cycle

add two method to SP:

boolean hasNegCycle();   
Iterable<DirectedEdge> negCycle();

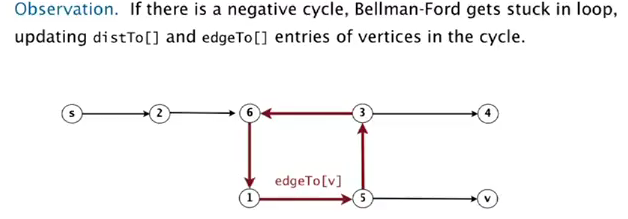
prop.

if a vertex u is updated in phase V, there exists a negative cycle, and can track edgeTo[u] to find the cycle.

原因是最短路径的长度小于V, 如果大于V则说明存在negative cycle.

negative cycle application

arbitrage detection

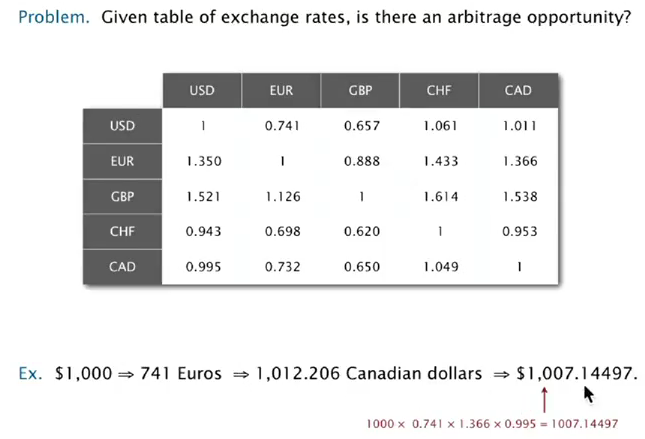
建模: graph of currencies, edge weight = exchange weight (complete graph).
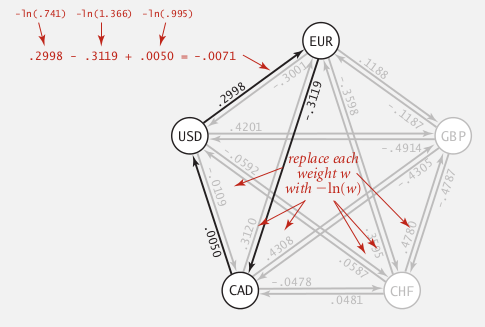
⇒ find a cycle whose product of edge is >1.
⇒ take logs to make a shortest-path pb.
⇒ take minus log, then try to find a negative cycle.

NB!!

Summery