1. Intro to digraphs

Has profound differences wrt undirected graphs.

def: digraph
edges: have directions
vertex: distinguish indeg and outdeg

digraph pbs:

• path/shortest path
• topological sort: Can you draw a digraph so that all edges point upwards?
• strong connectivity: Is there a directed path between all pairs of vertices?
• transit closure
• PageRank

2. Digraph API

public class Digraph{   
    Digraph(int V);   
    void addEdge(int v, int w);// edge is directed   
    Iterable<Interger> adj(int v);// vertices reached by outgoing edges   
    int V();   
    Digraph reverse();// <--new methode wrt undirected graph   
}

representation: adj-list, ie. an array of bags.
Bag<Integer>[] adj;// prec vertices

3. Digraph Search

BFS and DFS can be applied to digraphs.

• reachability

find all vertices reachable from vertex-s.
use the same DFS as for undirected graphs.
→ application: programme control-flow analyse, garbage collection.

• DFS is the basis for a lot of digraph pbs: 2-satisfiability, Euler path, strongly connected component.

• multiple source shortest path:

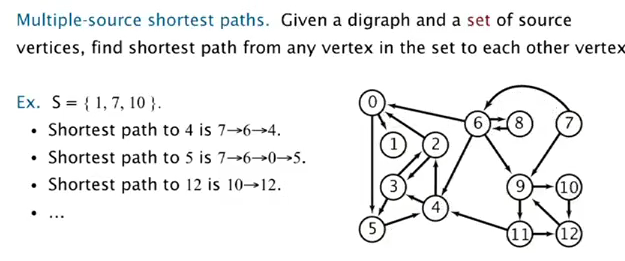
⇒ use DFS but enque all vertices in the set.
→ application: web crawler(DFS not suitable for crawling)

4. Topological Sort

application. precedence schedule, java compiler (cycled inheritance), ...

def. topo-order
is a permutation of vertices, where for each vertice v→w, w is behind v in the permutation.

def. DAG
directed acyclic graph.
prop. for a digraph, topological order exists iff graph is a DAG.

algo: ⇒ use DFS~
reverse DFS postorder

def. postorder
is the order of the vertices that we have finished (ie. we have visited all reachable vertices from this vertex).

implementation

这个以前的blog写过...

private boolean[] visited;   
private Stack<Integer> revPostorder;// stores the vertices in reverse post order   
private void dfs(Digraph G, int v){   
    visited[v] = true;   
    for(int w: G.adj(v))   
        if(!visited[w])   
            dfs(G, w);   
    //** now we know the vertex v is "finished" **   
    revPostorder.push(v);   
}   
public Iterable<Integer> topoOrder(Digraph G){   
    for(int v=0;v<G.V();v++)   
        if(!visited(v)) dfs(G,v);// visit all cc   
    return revPostorder;   
}

proof

prop. reverse post-order of a DAG is in topological order.
(这个证明蛮精彩)
pf.
for any edge v→w, when dfs(v) is called:

• case 1: dfs(w) is called and returned, so w is done before v in post-order;
• case 2: dfs(w) is not called, it will be (in)directly get called by dfs(v), so dfs(w) finishes before dfs(v);
• case 3: dfs(w) is called but NOT returned (ie, w not finished) → exist path from w to v ⇒ graph is not a DAG! (cycle detection)

5. Strong Components

For undirected graphs: connected components can be solved with dfs or UF.

def. Strongly-connected
v and w are strongly-connected if exist path from v to w and w to v.
→ is an equivalent relation.

def. Strong Component
subset of V where each pair are strongly-connected.

Goal: compute all strong components(scc) in a digraph.

linear time DFS solution: Tarjan (1972)

(developed version: a two-pass linear-time algorithm)

Intuition: scc for G is the same for G.reverse().

Kernel DAG: contract each scc into a single vertex.

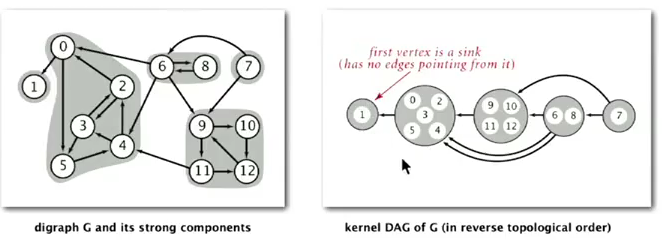
Idea:

• compute topological-order in the kernel DAG.
• run DFS, consider vertices in reverse-topo-order

[Algo]
1. compute topo-order in G.reverse (just a DFS in the reversed graph)
2. run DFS in original G, visit unmarked vertices in topo-order of G.reverse. (instead of visiting vertices by their index)

⇒ each time we finish a dfs from a vertex, we get a scc!
太精彩了!!!

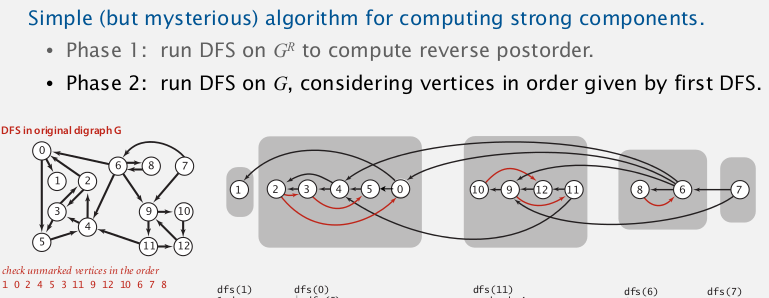
proof: tricky, cf book...(貌似Werner课上讲过..)

implementation

private int[] scc = new int[V]; // scc[v] is the index of the SCC that v belongs to   
private int sccCount = 0;   
private boolean[] visited = new boolean[V];   
public getSCC(Digraph G){   
    // 1. get topo-order in reverse graph   
    Iterable<Integer> topoOrderGR = topoOrder(G.reverse());   
    // 2. run dfs in original graph, run on vertices using the above topo-order    
    for(int v:topoOrderGR)// <-- only difference from the standard topo-order algo   
        if(!visited[v])   
            dfs(G, v, sccCount++);//increment sccCount everytime we done a component   
}   
private dfs(Digraph G, int v){   
    // run dfs from v, and all touched vertices are marked in sccId's SCC   
    visited[v] = true;   
    scc[v] = sccCount;   
    for(int w:G.adj(v))   
        if(!visited[w]){   
            scc[w] = sccCount;   
            dfs(G,w);   
        }   
}