[XCS224N] Lecture 7 – Vanishing Gradients and Fancy RNNs

Vanishing Gradient Intuition and Proof

ex: grad of loss at position 4 w.r.t.hidden state at postion 1

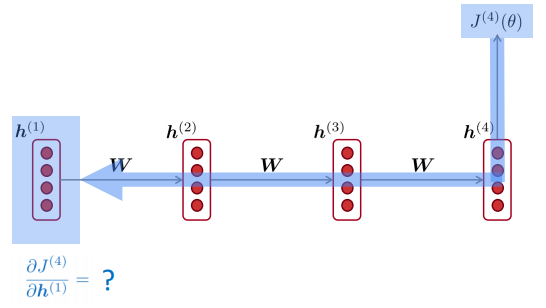
with chain rule, the grad is smaller as it backprops

⇒

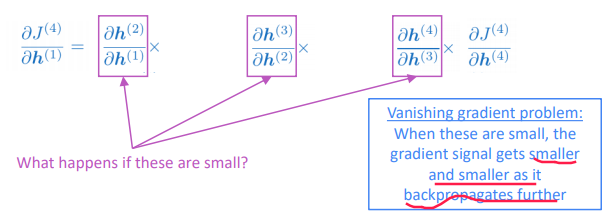
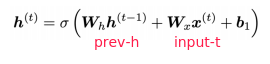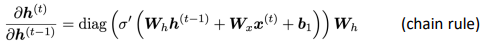
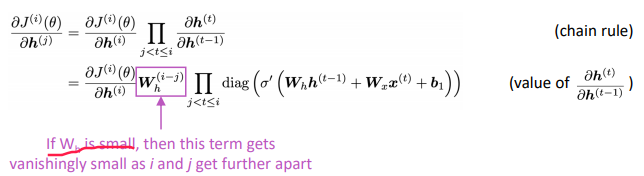
If the largest eigenvalue of Wh is less than 1, the gradient J_i/h_j will exponentially shrink.

Why Vanishing Gradient is a Problem

J2/h1 is bigger than J4/h1

Model weights are only updated only with respect to near effects, not long-term effects.

Gradient can be viewed as a measure of the effect of the past on the future.

example:

RNN models leans better sequential recency than syntactic recency.

Exploding Gradients

If the gradient is too big, SGD update step is too big ⇒ this will result in Inf or NaN in your network.

solution: gradient clipping

LSTM Overview

How to fix vanishing gradient:

In a vanilla RNN, the hidden state is constantly being rewritten

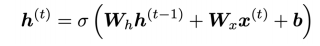
⇒ can we have an RNN with separate memory ?

⇒ LSTM

Idea:

• at step t , in addition to the hidden state h_t , have a cell state c_t
• both h_t and c_t are of length n
• cell states store long-term information
• the LSTM can erase, write and read information from the cell

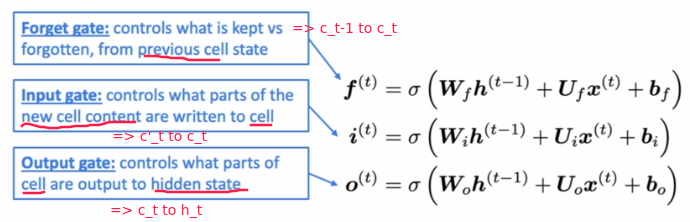
⇒ the selection of erase/write/read action is controlled by the corresponding gates:

• each gate is also vec of length n
• each timestep, each element of the gates can be open (1), closed (0), or somewhere in-between.
• open: info being passed through
• closed: info don't pass
• gates are dynamic: their value is computed based on the current context i.e.gate = sigmoid(W_hh_t-1 + W_xx_t + b)

The three gates: f, i, o

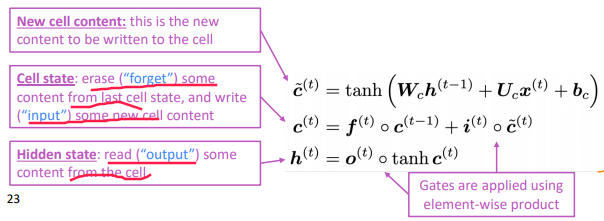
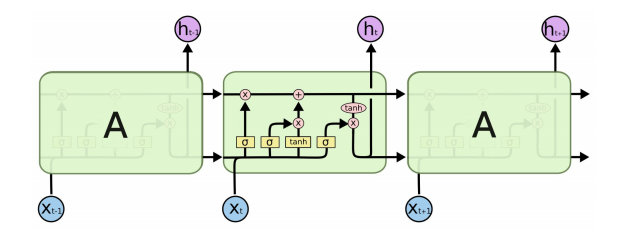
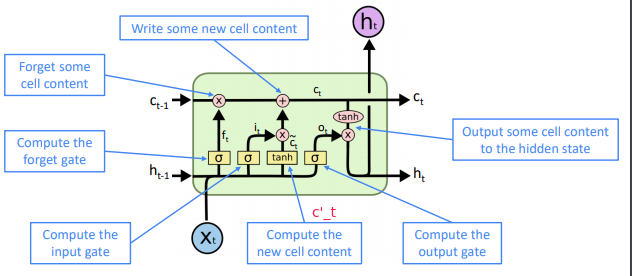
• LSTM architecture makes it easier for the RNN to preserve information over many timesteps

if forget gate f is always 1, the info in the cell is preserved indefinitely

• LSTM doesn’t guarantee that there is no vanishing/exploding gradient, but it does provide an easier way for the model to learn long-distance dependencies.
• Became successful in 2013-2015
• in 2019: other approaches (e.g.Transformers) have become more dominant for certain tasks

Gated Recurrent Units

Simpler alternative to the LSTM proposed in 2014.

Main idea:

• remove the cell state c_t, only use hidden state h_t.
• still using gates to control flow of information

gates:

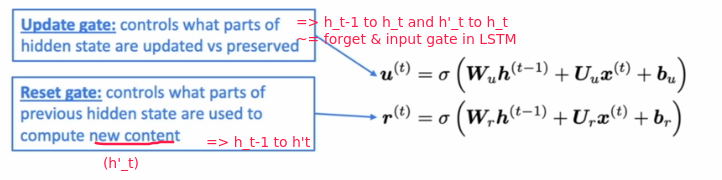
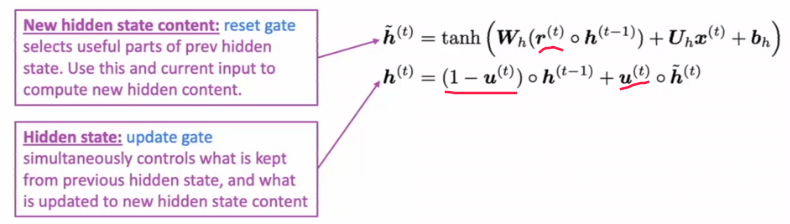
GRU makes it easier to retain info long-term (e.g. by setting update gate u to 0)

LSTM vs GRU

• LSTM and GRU are most widely used RNN variants
• more robust to vanishing gradient problem
• GRU is quicker to compute and has less params
• no conclusive evidence that one consistently performs better than the other
• LSTM is a good default choice (especially if your data has particularly long dependencies, or you have lots of training data)
• Rule of thumb: start with LSTM, but switch to GRU if you want something more efficient

Vanishing and Exploding Gradients in Other Architectures

Vanishing/exploding gradient is NOT just a RNN problem:

• It's a common pb for all deep NN architectures.
• But RNNs are particularly unstable due to the repeated multiplication by the same weight matrix
• The lower layers are learnt very slowly (hard to train).

⇒ solutoin: add more direct connections (thus allowing the gradient to flow)

ex1. "ResNet": residual connections (or skip-connections)

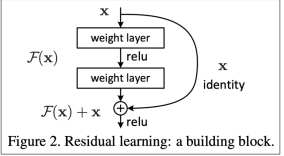
⇒ makes deep networks much easier to train

ex2."DenseNet" Directly connect everything to everything! (from all layers to all layers)

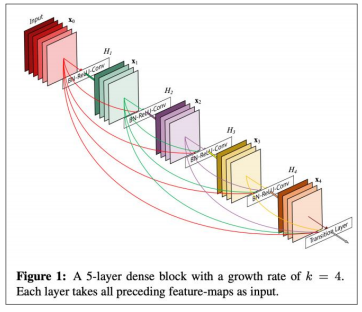
ex3."Highway connections" Similar to residual connections, but the identity connection vs the transformation layer is controlled by a dynamic gate

Bidirectional RNNs

task: sentiment classification using: RNN, and using elementwise max to get sentence encoding

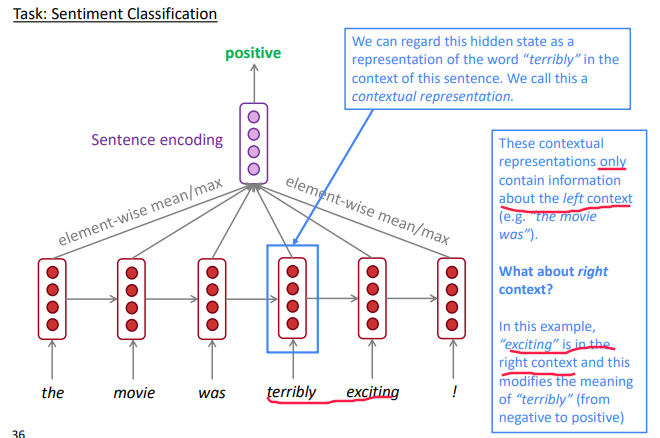
⇒ Bidir RNN: two separate RNNs, concat

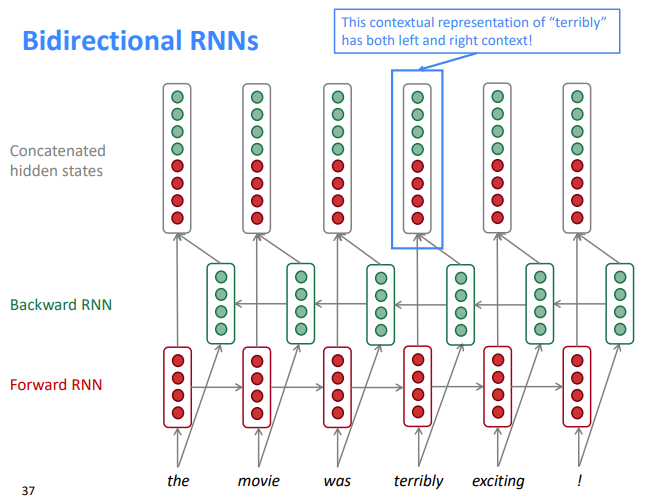
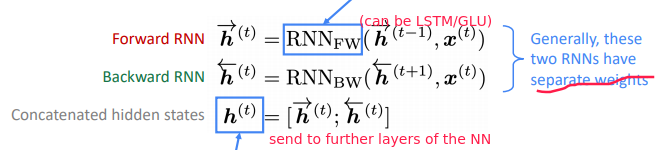
If you do have entire input sequence, bidirectionality is powerful (you should use it by default)

Multi-layer RNNs

Apply RNN in multiple layers

⇒ allows the network to compute more complex representations

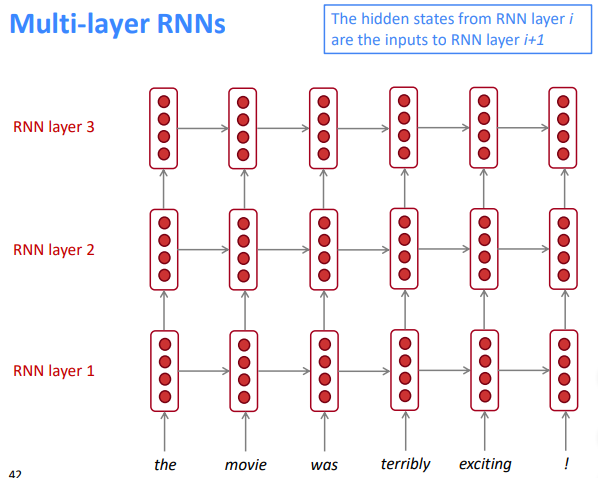
• (2017 paper): 2 to 4 layers is best for the encoder RNN, and 4 layers is best for the decoder RNN
• skip-connections/dense-connections are needed to train deeper RNNs (e.g. 8 layers)
• Transformer-based networks (e.g. BERT) can be up to 24 layers