This week: neural net fundamentals
Classification Setup and Notation
training data:
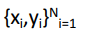
softmax classifier
(linear classifier — hyperplane):
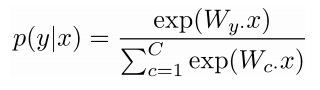
ith row of the param W: weight vector for class i to compute logits:
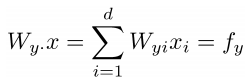
prediction = softmax of f_y:
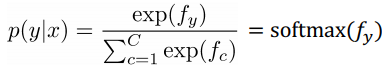
cross-entropy
goal: for (x, y), maximize p(y|x) ⇒ loss for (x, y) = -log p(y|x)
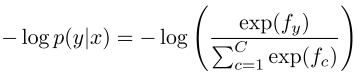

in our case, the truth distribution is one-hot , i.e.p = [0, 0, ... , 1, ... 0]
⇒ cross entropy H = - sum{log q(y|x), for all x, y}
loss for all training data = averaging the losses:
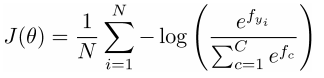
where the logits vector f is:
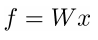
Neural Network Classifier
softmax or SVM or other linear models are not powerful enough ⇒ NN to learn nonlinear decision boundaries
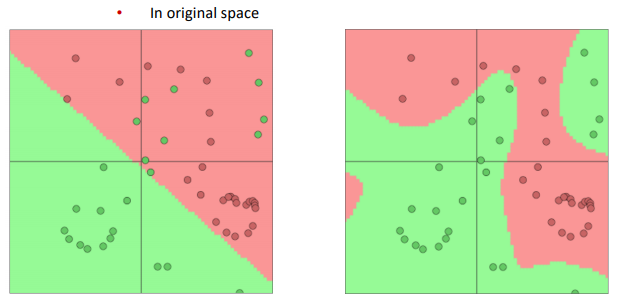
in NLP:
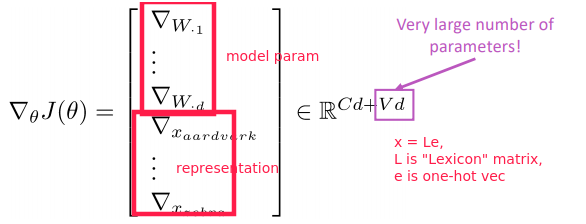
learn both model parameters ( W ) and representations (wordvecs x )
artificial neuron: y=f(Wx) , where f is nonlinear activation func.
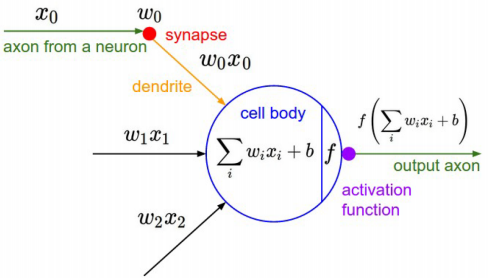
when f = sigmoid = 1/(1+exp(-x)) , the neuron is binary logistic regression unit.
A neural network = running several logistic regressions at the same time
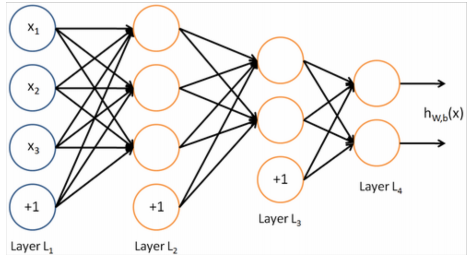
matrix notation:
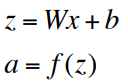
Without non-linearities f(), deep neural networks can’t do anything more than a linear transform.
Named Entity Recognition (NER)
task: find and classify names in text

BIO encoding:

Binary Word Window Classification
Classify a word in its context window of neighboring words. simple idea: concat all context words

Binary classification with unnormalized scores(2008&2011): build true window and corrupted windows.

feed-forward computation:

intuition: middle layer learns non-linear interactions between words: example: only if “museums” is first vector should it matter that “in” is in the second position.
max-margin loss: let true window score be larger (by at leaset delta=1)than the corrupted window score.

QUESTION: why we can use SGD when continuous?
SGD:
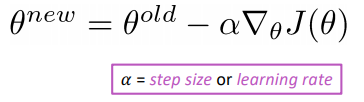
Computing Gradients by Hand
multivariable derivatives / matrix calculus
- *when f is from Rn → R1, *Gradient=vector of partial derivatives
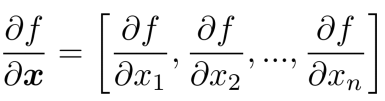
- when f is from Rn → Rm, Jacobian is an m x n matrix of partial derivatives

chain rule: multiply the Jacobians
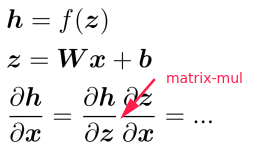
⇒ the nonlinear (activation) function h is element-wise, Jacobian of h is diagonal:

⇒ other Jacobians:
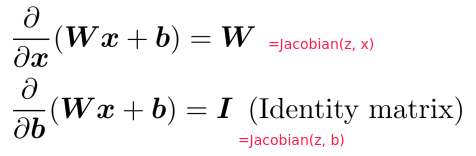
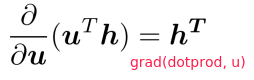
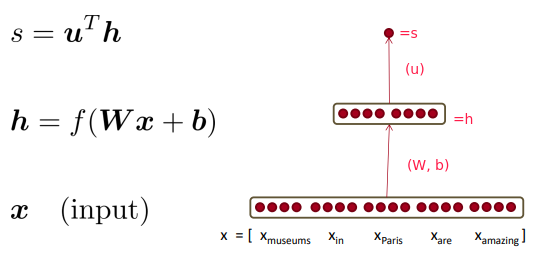
Gradients in Neural Network
notation:
⇒ Apply the chain rule with Jacobian/grad formulars from last section:
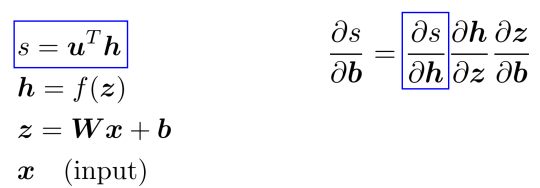

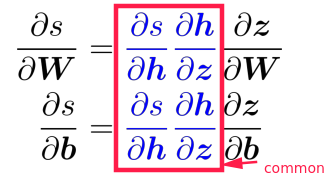
⇒ extract the common part, call it local error signal:
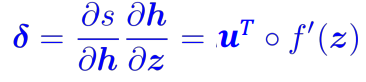
⇒
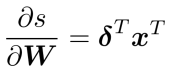
Part 3 of series «XCS224N: NLP with deep learning»:
- [XCS224N] Lecture 1 – Introduction and Word Vectors
- [XCS224N] Lecture 2 – Word Vectors and Word Senses
- [XCS224N] Lecture 3 – Neural Networks
- [XCS224N] Lecture 4 – Backpropagation
- [XCS224N] Lecture 5 – Dependency Parsing
- [XCS224N] Lecture 6 – Language Models and RNNs
- [XCS224N] Lecture 7 – Vanishing Gradients and Fancy RNNs
- [XCS224N] Lecture 8 – Translation, Seq2Seq, Attention
Disqus 留言