1. FUNCTIONAL EXPRESSIONS
syntax for functional expr: function some_identifier -> some_expr
the type of the functional expr is t1 -> t2 where t1 is the type of some_identifier, t2 is type of some_expr
ex.
function x -> x + 1;;
(function x -> 2*x) 5;; (*annonymous function*)
the previous way of defining function:
let f x = e,
is just an abbreviation for common let-binding:
let f = function x -> e
In fact, the most general form of a function definitoin contains a seq of pattern matching:
function
| pattern_1 -> expr_1
| pattern_2 -> expr_2
When only 1 pattern, the | is omitted.
example
let rc length = function
| [] -> 0
| _::r -> 1 + length r;;
type expr =
| Int of int
| Add of expr * expr;;
let rec eval = function
| Int n -> n
| Add(e1, e2) -> (eval e1) + (eval e2);;
2. FUNCTIONS AS FIRST-CLASS VALUES
functional types are just values of a particular type, thus this allows the uniform way of naming a value let x = ...
Types govern function application. We can apply e1 to e2 when:
- e1 has type t1 -> t2
- t1 matchs the type of e2

let f1 = [(function x -> x+1); (function x -> 2*x)];;
(List.hd fl) 17;;
let apply_twice f x = f (f x);;
apply_twice (function x -> 2*x) 1;;
let rec apply_n_times f n x =
if n<=0 then x
else apply_n_times f (n-1) (f x);;
apply_n_times (function x -> 2*x) 10 1;;
let compose f g = (function x -> f (g x));;
let fg = compose (function x->x+1) (function x->2*x) in
fg 10;;
function pitfalls
function apply from left to right (function application associates to the left):
exp1 exp2 exp3
is equivalent to: (exp1 exp2) exp3
let double = function x -> 2*x;;
double double 5;;
double (double 5);;
3. FUNCTIONS WITH MULTIPLE ARGUMENTS
anonymous function with several arguments: use keyword fun:
fun p1 ... pn -> exp
unlike function keyword, fun only admits one case/branch
remark: funs with several arguments are just abbrevations for single-argument functions that returns a function:
let f1 = function n -> (function x -> n+x);;
(f1 17) 73;;
f1 17 73;;
let f2 = fun n x -> n+x;;
f2 17 73;;
(f2 17) 73;;
in fact, fun x1 ... xn -> e is just abbreviation for: function x1 -> (..(function x2 -> ... -> (function xn -> e)..)
4. PARTIAL FUNCTION APPLICATION
let f = fun x y -> exp is equivalent to: let f = function x -> (function y -> exp)
⇒ partially apply f (ie, f x) will give a function.
let f1 = fun x y x -> x + y *z;;
let f2 = f1 1;;
let f3 = f2 2;;
f3 4;;
what happens at func-application:
when applying f = function x->e to a:
→ evaluate e in the context x=a
→ the arrow -> will block any evaluation
let f = fun x y -> (x / 0) + y;;
let f2 = f1 17;; (*error will not happen here, as the `->` blocks the evaluation!*)
f2 42;;
partial evaluation
sometimes we can do part of a calculation as soon as we have the frist few arguments
⇒ extract that part of calculation before the arrow !
let egal l1 l2 =
List.sort compare l1 = List.sort compare l2;;
let egalp l1 =
let l1sorted = List.sort compare l1 in (*sort the 1st argument before going to the next functional abstraction*)
function l2 -> l1sorted = List.sort compare l2;
5. MAPPING FUNCTIONS ON LISTS
many useful functions in the List module, either open List at beginning, or with pointed notation (List.hd)
implementation
let rec map f = function
| [] -> []
| h::r -> (f h):(map f r);;
map (function x -> x*x) [1;2;3;4;5];;
let map2 f l1 l2 = match (l1, l2) with
| [],[] -> []
| h1::r1, h2::r2 -> (f h1 h2)::(map2 f r1 r2)
| _ -> raise (Invalid_argument "List.map2");;
map2 (fun x y -> x+y) [1;2;3] [10;20;30];;
examples
example1: int vectors/matrices
row vector: int list
matrix: list of row vectors
turn infix operators into functions : using parentheses (+) (/) ( * ) ...(note: spaces are necessary for *, otherwise this turns into comments...
let vsum = List.map2 (+);; (* use partial application *)
vsum [1;2;3] [10;20;30];;
let msum = List.map2 (List.map2 (+));; (* nested partial application *)
msum [[1;2;]; [3;4]] [[10;20]; [30;40]];;
example2: get all sublists of a list
type: a' list -> 'a list list
write using induction:
let rec sublists = function
| [] -> [ [] ]
| h::r ->
let rp = sublists r
let appendh = function lst -> h::lst in
rp @ (map appendh rp)
6. FOLDING FUNCTIONS ON LISTS
- map: apping a unary function on list, all elements considered isolated.
- folding: combining all elements of a list using a binary operator.
- 2 different ways of folding: fold-left/fold-right
fold_right
fold_right: ('a -> 'b -> 'b) -> 'a list -> 'b -> 'b
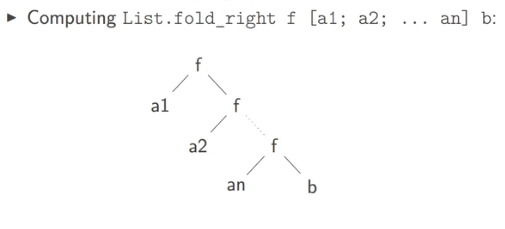
implementation and usage:
let rec fold_right f l b = match l with
| [] -> b
| h::r -> f h (fold_right f r b);;
fold_right (+) [1;2;3;4] 0;;
let concat = fold_right (fun x y -> x::y);; (partial application of fold_right)
concat [1;2;3] [3;4;5];;
fold_left
fold_left: ('a -> 'b -> 'a) -> 'a -> 'b list -> 'a
note: the default value's position is different from that of fold_right !
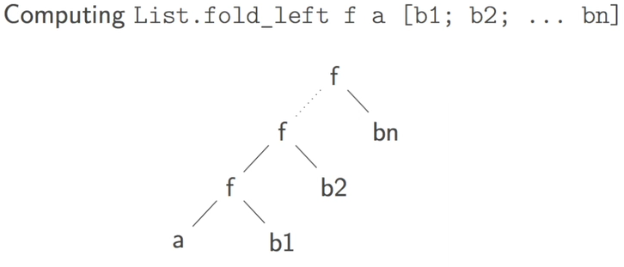
let rec fold_left f a l = match l with
| [] -> a
| h::r -> fold_left f (f a h) r;;
fold_left (+) 0 [1;2;3];;
let reverse = fold_left (fun x y -> y::x) [];; (* partial application *)
reverse [1;2;3;4];;
examples
example1: Inner product of int vectors
first get pairwise product, then sum up.
let product v1 v2 = List.fold_left (+) 0 (List.map2 ( * ) v1 v2);;
product [1;2;3] [4;5;6];;
example2: countif
let countif p l = List.fold_left
(fun acc elem -> if p elem then acc+1 else acc) 0 l;;
countif (fun x-> x>0) [3;1;-2;0;4];;
Part 5 of series «Introduction to Functional Programming in OCaml»:
- [OCaml MOOC] week0: intro and overview
- [OCaml MOOC] week1: BASIC TYPES, DEFINITIONS AND FUNCTIONS
- [OCaml MOOC] week2: BASIC DATA STRUCTURES
- [OCaml MOOC] week3: MORE ADVANCED DATA STRUCTURES
- [OCaml MOOC] week4: HIGHER ORDER FUNCTIONS
- [OCaml MOOC] week5: EXCEPTIONS, INPUT OUTPUT AND IMPERATIVE CONSTRUCTS
- [OCaml MOOC] week6: MODULES AND DATA ABSTRACTION
Disqus 留言