Last week, we only defined flat data structures which are nice to aggregate values but quite limited when you try to structure values.

This week: algebraic datatypes.

1. TAGGED VALUES

⇒ change the return type to a type query_result, which can be either of these:

• an error
• a new database (in case of successful insertion/deletion)
• a contact and its index (in case of successful search)

in ocaml, can define such a type (called sum type) by :

# type query_result =   
| Error  
| NewDatabase of database  
| FoundContact of contact*int;;  

More generally, to define disjoint union of types:

type some_type_identifier =   
| SomeTag of some_type  
| ...  
| SomeTag of some_type   

tag must start with uppercase letter

Taga are also called conscturcors, grammar is like java constructors: SomeTag (some_expr, ..., some_expr) (the parenthesis can be omitted if only 1 expr is required)

enumeration:

type color = Black | Gray | White;;

observing tagged values

must prvide an expression for each possible case of the value. A case is described by a pattern:
SomeTag (some_pattern, ..., some_pattern)

A branch is composed of a pattern an an expr separated by an arrow. some_pattern -> some_expr

pattern matching is a seq of branches:

match some_expr with  
| some_pattern -> some_expr  
|...  
| some_pattern -> some_expr   

example:

let engine db query =   
  match query with  
    | Insert contact -> insert db contact  
    | Delete contact -> delete db contact  
    | Search name -> search db name;;   

synatactic shortcut: function keyword (for functions with only 1 argument)

pitfalls

• ill-typed pattern
• non-exhaustive case analysis

These errors can be caught by the checker.

2. RECURSIVE TYPES

data structures with unbounded depth, ie, list/tree.

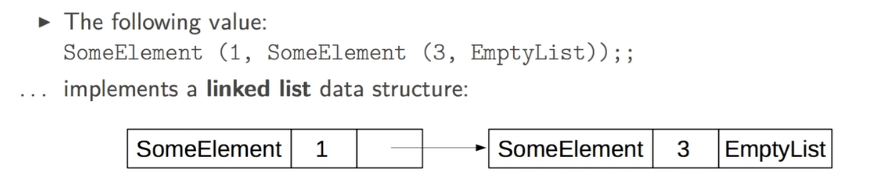
For example, an integer list can be defined as:

# type int_list =   
  | EmptyList  
  | SomeElement of int * int_list;;  
type int_list = EmptyList | SomeElement of int * int_list  

in the machine:

functions on such datastruct usually use pattern matching:

# let rec length = function  
  |EmptyList -> 0  
  |SomeElement (x,l) -> 1 + length l;;  
val length : int_list -> int = <fun>  

The predefined type in ocaml: t list

• empty list: [] ( [] is just a special tage corresponding to EmptyList)
• head and tail: i::r ( :: is just a special tage corresponding to SomeElement)
• a list can be defined by enumeration: [some_expr; ...; some_expr]
• list concatenation: @

# let rec length = function  
  | [] -> 0  
  | x::xs -> 1 + length xs;;  
val length : 'a list -> int = <fun>   
# length [1;2;3;];;  
- : int = 3  
# let rec rev = function  
  | [] -> []  
  | x::xs -> (rev xs)@[x];;  
val rev : 'a list -> 'a list = <fun>  
# rev [1;2;3;4];;  
- : int list = [4; 3; 2; 1]    

the rev function above has quad-complexity → here is the tail rec version:

# let rec rev_aux accu = function  
| [] -> accu  
| x::xs -> rev_aux (x::accu) xs;;  
val rev_aux : 'a list -> 'a list -> 'a list = <fun>  
# let rev l = rev_aux [] l;;  
val rev : 'a list -> 'a list = <fun>   

3. TREE-LIKE VALUES

the database type is formed in a (binary)tree-like fashion:

# type database =   
  | NoContact  
  | DataNode of database * contact * database;;  
type database = NoContact | DataNode of database * contact * database   

impose the BST invariant:

Now the functions insert/search/delete is BST fashion:

4. CASE STUDY: A STORY TELLER

type-directed programming: writing the right type declaration is half success.

define a story type (and other types:

type story = {  
  context: context;  
  perturbation: event;  
  adventure: event list;  
  conclusion: context;  
}  

and context = {characters: character list}  

and character = {  
  name: string;  
  state: state;  
  location: location;  
}  

and event =   
  | Change of character * state  
  | Action of character * action  

and state = Happy | Hungry  

and action = Eat | GoToRestaurant  

and location = Appartment | Restaurant;;   

5. POLYMORPHIC ALGEBRAIC DATATYPES

parametric programming: example — list is parametrized by the element type.
Hence in List module contains polymorphic functions.

Good for code reuse.

define your own polymorphic types, using 'a to indicate unkonw types:

type ('a1,...,1aN) some_type_identifier = some_type

example:

type 'a option =   
  | None   
  | Some of 'a;;  
type ('a, 'b) either =   
  | Left of 'a  
  | Right of 'b;;   
type square = {dimension: int);;  
type circle = {radius: int);;  
type shape = (square, circle) either;;  

another example: bst:

type 'a bst =   
  | Empty   
  | Node of 'a bast * a' * 'a bst ;;  

let rec insert x = function   
  | Empty -> Node (Empty, x, Empty)  
  | Node (l, y, r) ->   
    if x=y then Node (l,y,r)   
    else if x<y then Node (insert x l, y, r)  
    else Node (l, y, insert x r);;    

6. ADVANCED TOPICS

precise typing

when 2 types have the same structure but different semantical meaning: a sum type with only one constructor can be useful to distinguish them.

example:

type euro = Euro of float;;  
type dollar = Dollar of float;;  
let euro_of_dollar (Dollar d) = Euro (d /. 1.33);;  
let x = Dollar 4;;  
let y = Euro 5;;  
let valid_comparison = (euro of dollar x < y)   

disjunctive patterns

Use or-patterns to factorize branches into a unique branch:

some_pattern_1 | some_pattern_2 means observation of either pattern 1 or pattern 2.

constraint: both must contain the same identifiers.

ex:

let remove_zero_or_one_head = function  
  | 0::xs | 1::xs -> xs  
  | l -> l  
let remove_zero_or_one_head' = function  

| (0|1)::xs -> xs   
| l -> l   

as-patterns

convenient ot name a matched component: some_pattern as x ( if the value can be observed using some_pattern, name it x)

ex.

let rec duplicate_head_at_the_end = function  
  | [] -> []  
  | (x::_) as l -> l @[x]   

guard: pattern matching branch using when

a guard (some bool-expression) can add an extra constraint to a pattern:

ex.

let rec push_max_at_the_end = function  
  | ([] | [_]) as l -> l  
  | x::((y::_) as l) when x<=y -> x::(push_max_at_the_end l)  
  | x::y::ys -> y::push_max_at_the_end (x::ys);; (*when x>y, should permuate x and y*)