问题: 现在本地ssh连接eth的daint服务器, 连接需要进行两次ssh: 第一次本地连接到ela服务器, 第二次从ela再次ssh到daint. 现在配置本地的ssh代理使之可以一次完成.
第一步: 生成sshkey
ssh-keygen
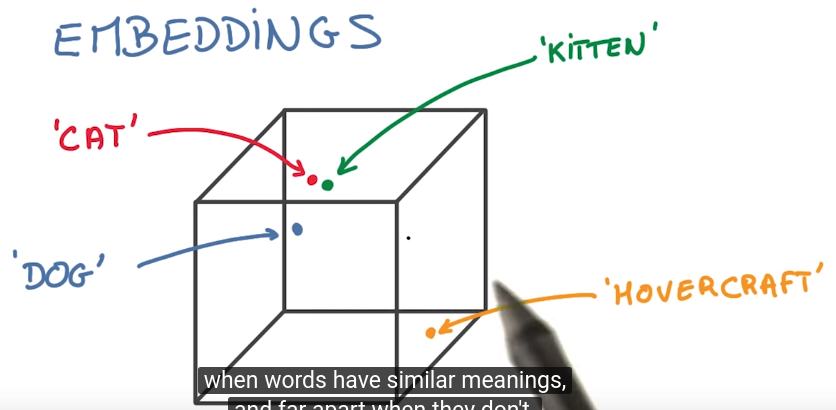
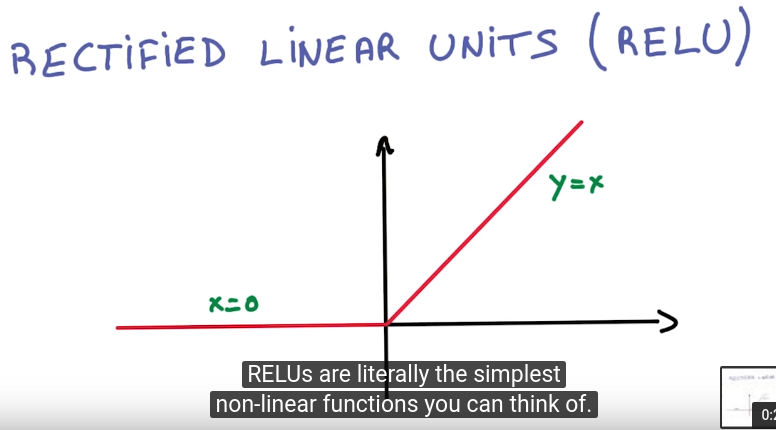
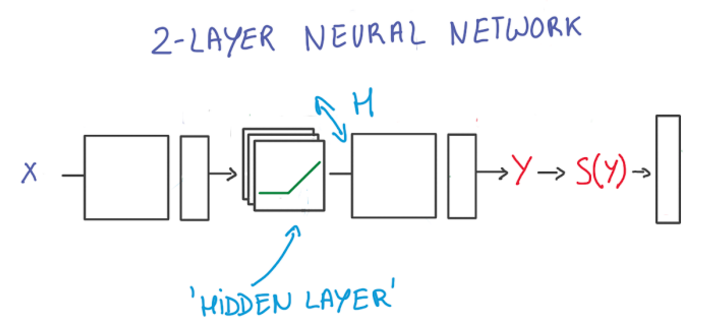
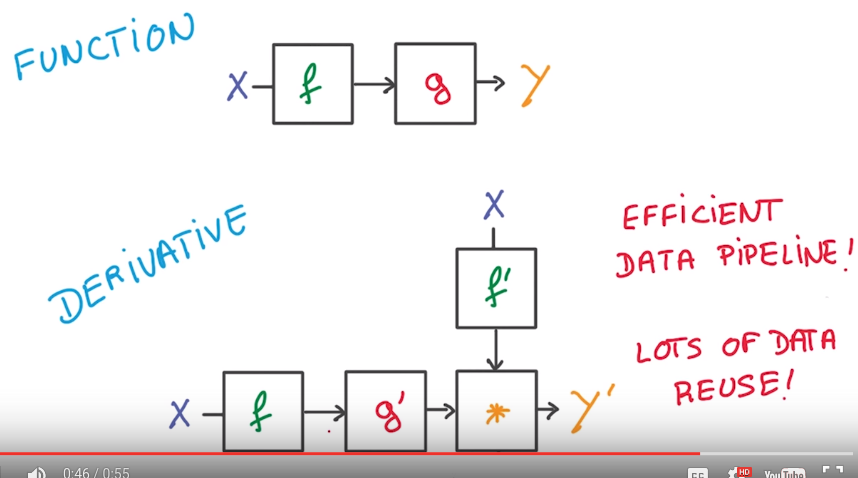
cat ~/.ssh/id_rsa.pub …4.1 - Objects Everywhere
scala is pure OO: every value is an obj, every operation is a method of obj.
scala.Int scala.Boolean maps to JVM standard primitive types.
Implement Boolean withous primitive type in scala:
Then defin false and true as objects, give implementation for ifThenElse() funciton:
object …This week, we'll cover traits, and we'll learn how to organize classes into hierarchies. We'll cover the hierarchy of standard Scala types, and see how to organize classes and traits into packages. Finally, we'll touch upon the different sorts of polymorphism in Scala.
3.1 - Class Hierarchies
abstract class
abstract …This week, we'll learn about functions as first-class values, and higher order functions. We'll also learn about Scala's syntax and how it's formally defined. Finally, we'll learn about methods, classes, and data abstraction through the design of a data structure for rational numbers.
2.1 - Higher-Order Functions
higher order functions …
In this week, we'll learn the difference between functional imperative programming. We step through the basics of Scala; covering expressions, evaluation, conditionals, functions, and recursion
1.1 - Programming Paradigms
imperative programming:
- modify mutable variables
- using assignments
- control structures: if-else, loops, break, continue, return, etc.
~~~> Von Neumann computer:
conceptualize data structures …
Get up and running with Scala on your computer. Complete an example assignment to familiarize yourself with our unique way of submitting assignments.
Tool setup
IntelliJ
use worksheet as a better REPL
SBT
navigate to the directory of the assignment you are working on, then start sbt.
(when first running …
problems with text:
- often very rare word is important, e.g. retinopathy
- ambiguity: e.g. cat and kitty
→ need a lot of labeled data ⇒ not realistic.
⇒ unsupervised learning
similar words appear in similar context.
embedding: map words to small vectors
measure the closeness by cosine distance:
word2vec
initial: random vector …
statistical invariance → weight sharing
e.g. image colors, translation invariance...
convnet
is NNs that share their weights across space.
convolution: slide a small patch of NN over the image to produce a new "image"
convnet forms a pyramid, each "stack of pincake" get larger depth and smaller area.
convolutional lingo …
Linear models
matrix multiplication: fast with GPU
numerically stable
cannot cocatenate linear units → equivalent to one big matrix...
⇒ add non-linear units in between
rectified linear units (RELU)
chain rule: efficient computationally
back propagation
easy to compute the gradient as long as the function Y(X) is made of simple blocks …
这是udacity上deeplearning的笔记, 做得非常粗糙, 而且这门课也只是介绍性质的... https://www.udacity.com/course/deep-learning--ud730
Softmax function
socres yi ⇒ probabilities pi
property: smaller scores ⇒ less certain about result
Onehot encoding
Cross entropy
measure how well the probability …