[Sequential Models] week2. Natural Language Processing & Word Embeddings

I - Introduction to Word Embeddings

Word representation
So far: representing words with one-hot encoding → word relationships are not generalized.
⇒ want to learn a featurized representatin for each word as a high-dim vector

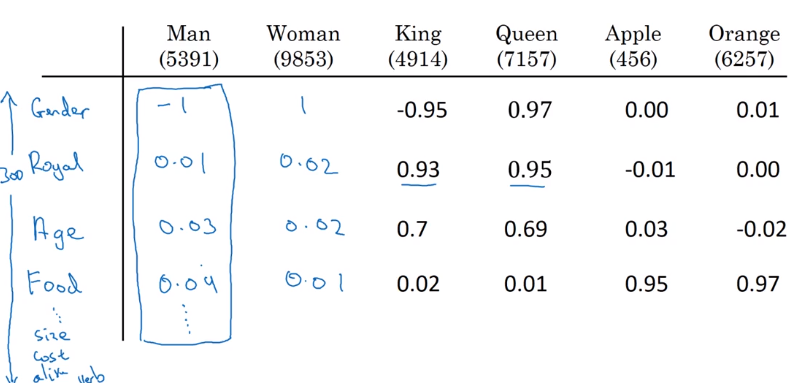
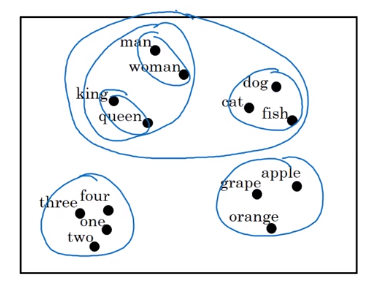
→ visualize word embeddings in 2-dim space, e.g. via t-SNE

Using word embeddings

example: NER
transfer learning: using pretrained embeddings

• learn word embeddings from large text corpus (or download pre-trained embeddings)
• transfter embedding to new task with smaller training set
• (optional) fine-tune word embeddings with new data

Word embedding ~ face encoding(embedding) in previous words.

Properties of word embeddings

Analogy reasoning of word embeddings.
e.g. man->woman as king->?
Embedding vectors have the relationship: e_man - e_woman ~= e_king - e_queen
Finding nearest neighbor (according to cosine-similarity).
examples:

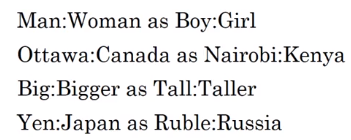
Embedding matrix

learning an embedding matrix E of shape (embed_dim, vocab_size)
e.g. embed_dim=300, vocab_size=10000
notataion:
o_w = one-hot encoding of a word w, dim=(10000,1)
→ e_w = E * o_w, dim=(300,1)

→ Learn E by random-init & gradient descent.
(In practice: use lookup function instead of matrix multiplication.)

II - Learning Word Embeddings: Word2vec & GloVe

Learning word embeddings

Some concrete algos to learn embedding matrix E. Start with complex algos and show simpler algos with good result.
e.g. Neural language model, i.e. predict next word in the sequence.
with fixed window size(e.g. =4), predict next word. Context=last 4 words, target=next word.

→ Using gradient-descent to update params (E, W, b).

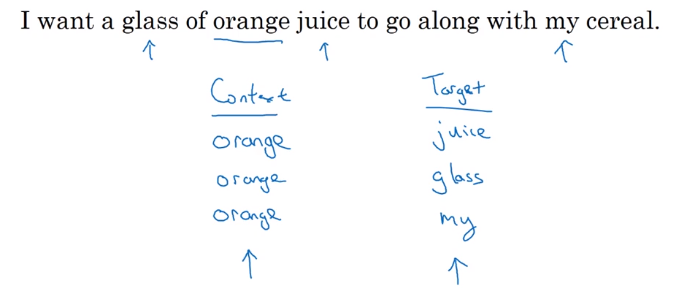
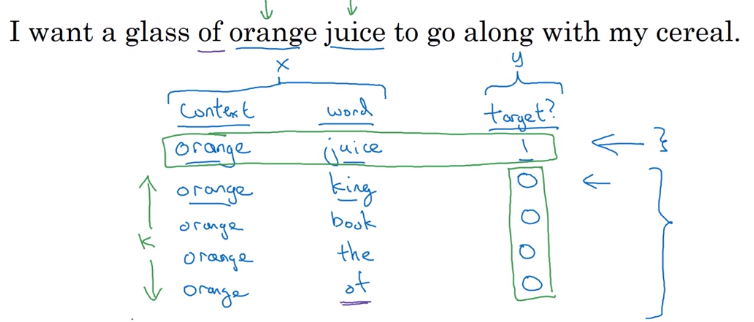
Other kinds of (simpler) context/targets:

• context=4 words to the left & right, target=the word in the middle
• context=previous word, target=next word
• context=nearby 1 word (skip-gram model)

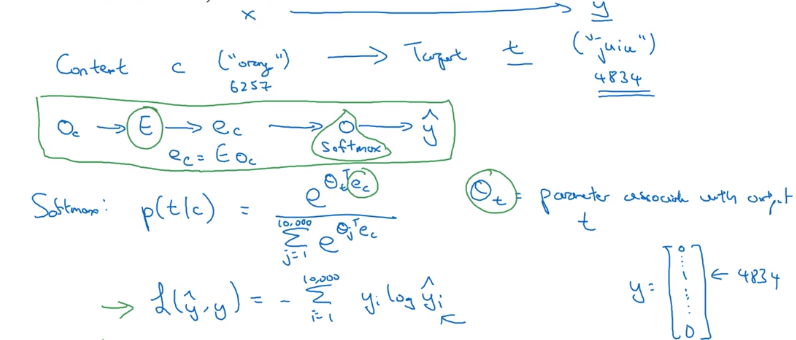
Word2Vec

Skip-grams
supervised problem: context/target pairs, given context word, predict target word
(|v| classes in total) → softmax

• context c: randomly pick a context word
• target t: randomly pick a target word in +/- 4 word window.

Skip-gram Model
model: context c -> onehot o_c -(E)-> embedding e_c → softmax → prediction yhat
→ target word y
loss = cross-entropy(y, yhat) / log-loss(y, yhat)

how to sample context c
uniform sampling for c: frequent words might dominant the training set.
→ heuristics to sample less common words via P(c).p

problem with skip-gram model
slow speed: to compute p(t|c) with softmax → involves summing up all 10000(vocab_size) logits in denominator of sotmax:

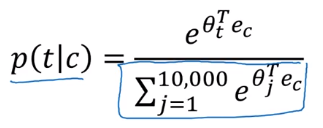
• method 1: using hierachical softmax: split all vocabs into buckets/binary trees — log(|v|) instea of O(|v|)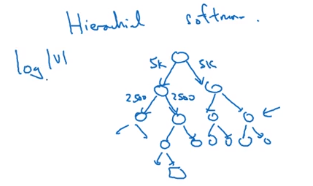
• method 2: negative sampling, modify training objective

Negative Sampling

To simplify the computation of softmax denominator: a different learning problem.
new learning problem
given a pair of word → predict if this pair is a context/target pair.
— binary classification instead of |v| classes.

• positive examples: sampled as before (sample context word c, then sample target word t in word window)
• negative examples: sample context word c, then pick rand word t from dictionary. Sample k=5~20 negative examples for each context word c.

Model: logistic regression
For context word c, there are |v|=10000 potential binary classification problems to train
→ and we train only (k+1) of them.
negative sampling: trun 10000-way softmax problem into 10000 binary classification problems, and each iteration only train k+1 of them.

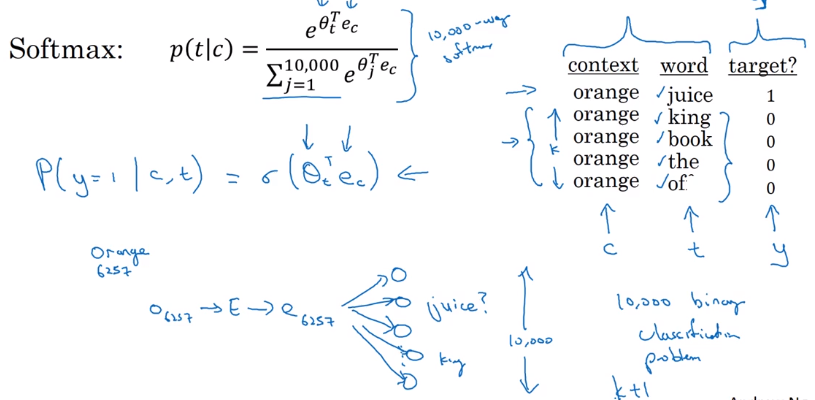
How to sampling negative examples

• sample according to empirical word frequence P(w) ~= tf(w) → might have a lot stop words sampled
• sample uniformly: P(w) = 1/|v|
• empirical best-choice: P(w) = tf(w)^0.75 / sum(tf(w')^0.75)

GloVe word vectors

GloVe(Global Vectors for word representation): even simpler than negative sampling.
previously: sampling skip-grams, i.e. pairs of words (c,t)
glove: Count appearance of co-occurrence, X_ij = #(i in the context of j).

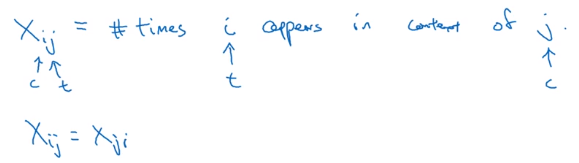
GloVe Model
Trying to approximate theta_i*e_j to -logX_ij, by solving theta_i and e_j.

• add weighting term f(X_ij) = 0 if X_ij=0, (0*log0 = 0), and f gives more weight to less frequent words
• theta_i and e_i are symmetric in optimization ⇒ final embedding e_i = (e_i+theta_i)/2

Featurization view of word embeddings
Learning embeddings are not guaranteed to align with featurized components in each axis.

III-Applications using Word Embeddings

Sentiment Classification

mapping a piece of text into a rating
simple model
sum/average all word embedding vectors as feature vector → pass to softmax clf.
pb: ignoring all word order

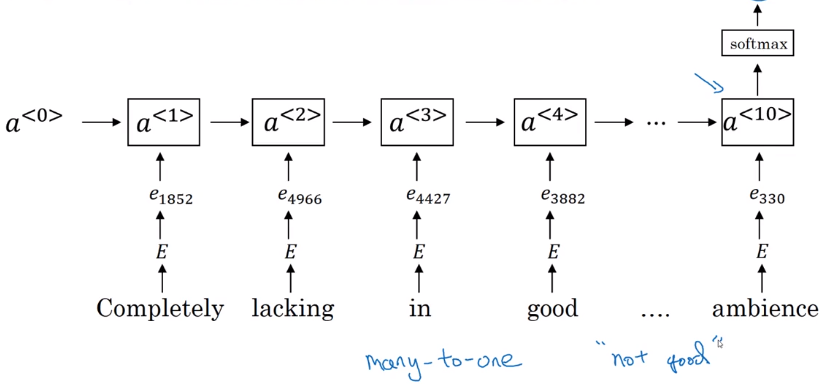
RNN model
take embedding vectors → sequence embedding matrix → feed to RNN
→ using last step output and feed to softmax.

Debiasing word embeddings

Eliminate biases in word embeddings, e.g. gender bias, due to biases in training text.

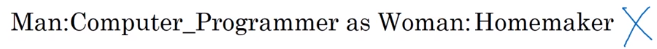
• Dentify bias direction: e.g. gender bias

take differences of vectors: e.g. e_he - e_she, e_male - e_female
→ find bias and non-bias directions

• Neutralization: project embeddings (of non-definitional words) to non-bias directions
• Equalize pairs: for definitional words(e.g. grandmother/grandfather, boy/girl), let them be equally-distant to axis

→ How to find defnitional words: train a classifier.